Trois jours de stage et six heures de train pendant lesquelles j'ai dévoré ce livre. Gilles Dowek a reçu le Grand Prix de Philosophie 2007 décerné par l'Académie Française. Je ne connais pas les autres lauréats mais pour ce qui est de ce livre je pense que la philosophie a vraiment trouvé du grain à moudre pour quelques années dans ces métamorphoses numériques.
Trois jours de stage et six heures de train pendant lesquelles j'ai dévoré ce livre. Gilles Dowek a reçu le Grand Prix de Philosophie 2007 décerné par l'Académie Française. Je ne connais pas les autres lauréats mais pour ce qui est de ce livre je pense que la philosophie a vraiment trouvé du grain à moudre pour quelques années dans ces métamorphoses numériques.
Au début du livre, j'étais en territoire connu mais j'ai déjà lu beaucoup de livres sur l'histoire des mathématiques alors j'ai pensé, tiens encore une histoire des maths. C'est vrai pour le tout début du livre mais la première partie est nécessaire à quiconque ne maîtrise par bien ce sujet afin d'introduire la logique des prédicats.
Et puis dès la cinquantième page, je vois apparaître mon copain Kant et ses jugements synthétiques à priori. Alors je commence à me dire que ça va cogner. On pourra d'ailleurs lire le documents suivant : La philosophie des mathématiques de Kant . Quel est le problème?
Kant propose deux types de jugements :
Analytique si une proposition est vraie par définition comme "un triangle à trois cotés".
Synthétique si la propostion est vraie sans que ce soit une définition. Par exemple "La terre a un satellite" . Ce jugement peut être a priori si on peut le concevoir dans la tête ou a poseriori s'il faut une intéraction avec la nature.
Les jugements analytiques semblent quant à eux exclusivement à priori.
Pour Kant le raisonnement se situe dans les jugements synthétiques à priori mais c'est là que ça coince par ce que ce n'est pas aussi simple que ça!
Le "simple", 2+2=4 pose problème. Frege va d'ailleurs montrer que 2+2=4 peut se déduire de la définition des nombres entiers et doit être classé parmi les jugements analytiques et non parmi les jugements synthétiques à priori.
On voit déjà poindre à l'horizon une problématique philosophique centrale concernant les mathématiques, leur constitution et leur évolution. Se constituent-elles au sein d'elles mêmes auquelles cas elles sont analytiques à partir des simples définitions. Relèvent-elles du jugement synthétique à priori ou doivent-elles aller chercher des éléments dans la nature pour se construire.
Il est inutile de vouloir répondre simplement à ces questions qui dépendent de l'évolution des mathématiques elles mêmes dont le pivot central est certainement la thèse de Church des années 30, affirmant l'identité entre la notion de calcul "informatique et la notion "commune " de calcul que nous avons.
En avançant encore un peu dans le livre on voit apparaitre l'idée selon laquelle Démonstration = Algorithme et puisque la thèse de Church nous donne Algorithme = Calcul, on a donc l'identité Démonstration = Calcul. Il devient donc nécessaire de distinguer les notions de démontrable et d'explicatif, ce qui est loin d'être facile pour les mathématiciens. La longueur des démonstrations est aussi abordée, avec par exemple la problèmatique suivante : Peut-on démontrer qu'un problème démontrable possède une démonstration "courte"?
Philosophiquement le sujet est dense!
D'autant qu'à la fin de l'histoire une surprise de taille nous attend avec un retour nécessaire à la nature... Mais je n'en dis pas plus.
Ce qui m'a aussi passioné dans le livre est le traitement du rapport du mathématicien et de la machine, de ce nouvel outil qui lui est maintenant indispensable. L'auteur s'interroge aussi sur le fait que l'ordinateur du mathématicien est le même que celui de Mme Michu, sauf bien sûr si les calculs sont vraiment très très longs et demandent un super-calculateur pour pouvoir être faits en un temps "raisonnable". Il est intreressant de comprendre quelles est la place de l'ordinateur-machine à coté du mathématicien-humain.
J'ai extrait quelques courtes citations vers la fin du livre qui me semblent assez explicites sur les métamorphoses du calcul qui est le sujet du livre et donc des mathématiques elles-mêmes:
En 1976, les mathématiques sont entrées dans la période instrumentée de leur histoire. Les instruments utilisés par les mathématiciens, ne sont pas des instruments qui prolongent les facultés de nos sens, mais qui prolongent les capacités de notre entendement: notre faculté de raisonner et surtout, de calculer. ( p 182 )
L'utilisation d'instruments commence, de même à changer, les mathématiques. ( p 182 )
La maquette sur laquelle on fait l'essai est donc une machine à résoudre un problème mathématique,[...] (p 188)
L'entrée des mathématiques dans leur ère instrumentée incite donc, non à accorder une confiance excessive dans les instruments utilisés, mais à restreindre prudemment la confiance parfois exagérée, que nous avons en nous-mêmes: nous aussi nous pouvons faire des erreurs. ( p 191 )
Podcast de Gille Dowek sur le livre et sur Canal-Académie
Pour compléter :
Des p'tits problèmes de coloriage ( autour du théorème des quatre couleurs)

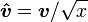 Alors que je consultais paisiblement mon Google Reader, je fus interpelé par un article intitulé "Fast inverse square root", partagé par un internaute du Monde. Je connaissais bien la traduction en français de tous les mots du titre: "Racine carrée inverse rapide". Chacun d'entre eux faisait sens mais lorsqu'ils étaient placés ensemble, je me retrouvais dans l'incapacité de prédire un contenu possible de l'article en question. J'imaginais bien sûr qu'il devait s'agir d'une méthode, exotique ,ça je ne le savais pas, mais certainement numérique pour calculer l'inverse d'une racine carrée de façon rapide.
Alors que je consultais paisiblement mon Google Reader, je fus interpelé par un article intitulé "Fast inverse square root", partagé par un internaute du Monde. Je connaissais bien la traduction en français de tous les mots du titre: "Racine carrée inverse rapide". Chacun d'entre eux faisait sens mais lorsqu'ils étaient placés ensemble, je me retrouvais dans l'incapacité de prédire un contenu possible de l'article en question. J'imaginais bien sûr qu'il devait s'agir d'une méthode, exotique ,ça je ne le savais pas, mais certainement numérique pour calculer l'inverse d'une racine carrée de façon rapide.