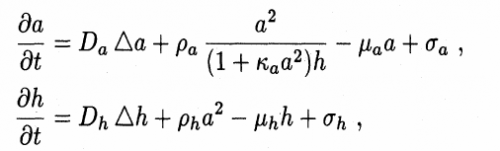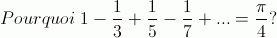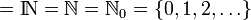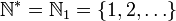L'objectif de ce billet est de se demander s'il peut exister une théorie générale des questions "Pourquoi?", ou de l'explication en général, de montrer que des philosophes et des scientifiques s'intéressent à cette question, et d'essayer de comprendre en quels termes est-ce qu'elle peut se formuler, quelles sont les difficultés liées à son élaboration. On ne pourra bien sûr pas traiter la totalité de ce sujet dans un simple billet de blog, compte tenu de l'ampleur de la tâche, de sa difficulté, du fait que l'on ne dispose certainement pas actuellement des bases théoriques suffisantes et aussi, signalons-le, des limites vite atteintes de l'auteur!
Les questions "Pourquoi?"
 Lorsque l'on demande à Teddy et Valentin, "Pourquoi les léopards ont-ils des tâches?", voilà ce qu'ils répondent:
Lorsque l'on demande à Teddy et Valentin, "Pourquoi les léopards ont-ils des tâches?", voilà ce qu'ils répondent:
L’histoire se passe dans la jungle, en Afrique. Nous sommes le 31 mars, avec trois meilleurs amis. Il y a Benji, un jeune léopard sans tâches, Chita et Kikou, ses deux amis singes. Comme chaque jour, ils jouent à trap-trap et à courir dans la jungle. Chita et Kikou adorent se cacher ou se percher dans les arbres. Mais Benji a beaucoup plus de mal pour les attraper. Eux, ils sont habitués à grimper et à sauter d’arbre en arbre. Pour Benji, il faut courir plus et user beaucoup d’énergie pour grimper dans l’arbre où se trouvent ses amis.
Chita et Kikou, très farceurs, décident de faire une farce à leur ami pendant sa sieste. Ils lui mettent des tâches de peinture noire sur son pelage. Benji se réveille et ne remarque rien. Il part à la recherche de ses amis. Mais il se pose des questions : « Pourquoi tout le monde me regarde et rie quand je passe ? » Arrivé au bout de la jungle, il retrouve Chita et Kikou. Ils tiennent un bout de miroir et se tordent de rire. Benji sursaute de peur quand il se voit avec son pelage tout tacheté de noir. Il comprend pourquoi les habitants rigolaient. Voyant leur ami triste, Chita et Kikou disent : « Poisson d’avril ! » Chose qu’ils ne savent pas, c’est que c’est de la peinture indélébile. Du coup, Benji rit aussi, il aime son nouveau look. Surtout depuis que les jeunes léopards l’admirent ! Voila pourquoi les léopards ont des tâches. On trouvera d'autres réponses d'enfants à la question "Pourquoi?" ICI.
Lorsqu'on pose la même question au scientifique voilà l'un des éléments principaux de la réponse qu'il propose, et l'on est bien loin de celle de Teddy et de Valentin:
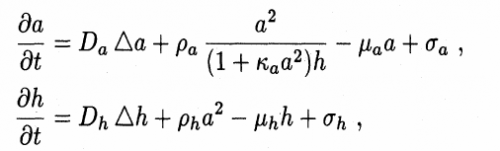
Une réponse intermédiaire entre le conte et la modélisation mathématique, serait le récit du vulgarisateur:
Ce qui est étonnant et remarquable, c'est que l'équation mathématique montre que les différents motifs de pelage dépendent seulement de la grosseur et de la forme de la région où ils se développent. Autrement dit, la même équation de base explique tous les motifs. Mais alors, pourquoi les tigres et les léopards ont-ils des motifs différents puisque leurs corps sont très similaires ? Parce que la formation des motifs ne se produirait pas au même moment durant la croissance de l'embryon.
Dans le premier cas, l'embryon serait encore petit et, dans l'autre cas, il serait déjà beaucoup plus gros. Plus précisément, l'équation montre qu'il ne se forme pas de motif si l'embryon est très petit, qu'il se forme un motif rayé si l'embryon est un peu plus gros, un motif tacheté s'il est encore plus gros, et ... aucun motif s'il est trop gros !
Voilà pourquoi la souris et l'éléphant n'auraient pas de taches !
A travers cette question, il semble flagrant que la question du "Pourquoi?" est relative, que la connaissance de l'interlocuteur est fondamentale. Une théorie du "Pourquoi?" pourra-t-elle se constituer indépendamment de celui-ci?
Un autre type de question va faire apparaître une nouvelle difficulté. Par exemple on peut se demander: "Pourquoi Adam a-t-il mangé la pomme?"
La première idée qui viendrait à l'esprit est de considérer que cette question est du domaine religieux et qu'elle ne trouvera aucune réponse. Si cette remarque est vraie et renvoit la problématique vers la construction des mythes fondateurs, il n'en reste pas moins que si l'on tente d'y répondre, force est de constater que son ambiguité n'est pas religieuse mais, bel et bien, sémantique.
On peut en fait répondre à "Pourquoi Adam a-t-il mangé la pomme?". La problématique implicite étant de répondre à la question "Pourquoi lui?".
On peut aussi répondre à "Pourquoi Adam a-t-il mangé la pomme?", la problématique implicite étant maintenant de savoir pourquoi cette action a été réalisée et non une autre, comme l'écraser, la donner, la cacher.
Il reste une dernière interrogation du type "Pourquoi Adam a-t-il mangé la pomme?", sous entendu, pourquoi ce fruit, pourquoi un fruit?
Contrairement à l'exemple précédent où la connaissance de l'interlocuteur avait une place capitale une fois que la question était posée, dans ce cas présent, c'est la question elle-même qui peut être ambigüe, trop lâche. Il paraît donc important de se prémunir devant ces ambiguités en formulant une question "Pourquoi?" satisfaisante permettant d'assurer une réponse pertinente. Il est important de connaître l'angle d'attaque de la réponse satisfaisante. Mais est-il possible de construire ce type de questions? Là aussi c'est un point incontournable de la possibilité de formuler une théorie du "Pourquoi?".
Dans le domaine mathématique, des questions "Pourquoi?" peuvent aussi apparaître, comme par exemple :
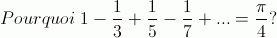
Le problème qui se pose ici est encore d'un autre niveau que les deux précédents. Il s'agit de comprendre que ce n'est pas parce qu'une chose est vraie et qu'elle est prouvée, qu'elle est expliquée. Le résultat énoncé plus haut est vrai mais la question est de savoir "Pourquoi est-ce que c'est Pi/4 qui se trouve à droite de l'égalité et pas un autre nombre?", sous entendu quel est le lien explicatif entre le membre de gauche et celui de droite? On va donc voir arriver un gros problème avec le statut de la démonstration mathématique et du calcul. Démonstrations et calculs ne sont pas tous explicatifs. La démonstration, le calcul ne répondent pas de façon inconditionnelle à la question du "Pourquoi?". Dans le champ des mathématiques, une théorie du "Pourquoi?" ne pourra pas se contenter de l'existence d'une démonstration valide ou d'un bon calcul.
Si l'on reste dans le domaine des mathématiques, un autre type de question "Pourquoi?" pose problème. C'est celle qui demande pourquoi est-ce que l'on fait tel type de chose pour faire une démonstration? Par exemple "Pourquoi introduire la fonction "machin" pour démontrer le résultat "truc"? Et le professeur de mathématiques ne s'y trompe pas car sa réponse est presque toujours invariable même si elle n'est en rien explicative "On fait ça parce que ça marche!". On voit donc bien qu'il y a là une difficulté réelle qui aborde la naissance des idées, la justification de l'intuition, la justification d'une étape "deus ex machina".
D'autres questions "Pourquoi?" peuvent aussi s'avérer problématiques, comme par exemple: "Pourquoi JFK est-il mort le 22 novembre 1963?". Une fois levées les ambiguités de la question sur les attentes (JFK, mort ou date), il est ici question de l'explication historique. L'histoire ne se répétant pas, peut-on concevoir une "explication historique". L'explication relevant principalement de la rationnalité et de la science, n'est-on pas dans l'incapacité d'expliquer l'histoire, sauf à la considérer comme science, ce qui n'est pas sans apporter un autre lot de difficultés?
Les questions exclusivement scientifiques ne sont pas non plus sans poser de problème!
Y a t'il une meilleure explication que les autres à cette question : "Pourquoi aucun observateur ne peut se déplacer plus vite que la lumière ?" ?
"Pourquoi les lois de Kepler sont-elles valides ?" Le "vrai" physique, comme nous l'avons vu juste au dessus, n'épuise pas à lui seul la question du "pourquoi".
Derrière ces quelques "questions-pourquoi", nous voyons pointer la difficulté de concevoir une théorie qui permettrait d'englober toutes les réponses possibles et de sélectionner parmi elles, celle qui est la plus pertinente. Cette théorie devra de plus nécessairement contenir les "questions-pourquoi" des mathématiques. La réponse au "Pourquoi?" se devant d'être explicative, il faudra se confronter à la nature de l'explication qui soulignons-le, ne peut pas éliminer le récepteur, introduisant ainsi une forte part de relativité, bien inconfortable en sciences par exemple.
Pouvons-nous concevoir une théorie du "Pourquoi?"? Est-il possible de la mathématiser, et est-elle compatible avec les mathématiques? Pour préciser les choses , la théorie des questions-pourquoi impose que le particulier puisse se déduire de la règle. Cela exige aussi de savoir s'il est possible de lever toutes les ambiguïtés associées à ce type de question, comme nous pouvons le constater dans les questions sur Adam et la pomme. Il faut aussi se poser la question, si l'on choisit d'associer la meilleure explication à la meilleure probabilité de certitude, de savoir si la démonstration mathématique (de probabilité 1) est toujours explicative. Il faut aussi se poser la question de savoir si l'on parvient à expliquer le "Pourquoi faire cela?" en vue d'une démonstration, plutôt qu'autre chose, mettant ici de l'arbitraire là où il ne devrait pas y en avoir.
Lire la suite
 Certains mathématiciens refusent l'idée que l'infini puisse être un concept que l'on peut utiliser. Ce sont les finitistes. Les plus radicaux d'entre eux sont les ultrafinitistes dont faisait partie le mathématicien russe Alexander Yessenin-Volpin, logicien et poète ( qui a été interné dans un hopital psychiatrique en 1949 pour "poésie anti-soviétique" !).
Certains mathématiciens refusent l'idée que l'infini puisse être un concept que l'on peut utiliser. Ce sont les finitistes. Les plus radicaux d'entre eux sont les ultrafinitistes dont faisait partie le mathématicien russe Alexander Yessenin-Volpin, logicien et poète ( qui a été interné dans un hopital psychiatrique en 1949 pour "poésie anti-soviétique" !). Lorsque l'on demande à Teddy et Valentin, "Pourquoi les léopards ont-ils des tâches?", voilà ce qu'ils répondent:
Lorsque l'on demande à Teddy et Valentin, "Pourquoi les léopards ont-ils des tâches?", voilà ce qu'ils répondent: