O est-il un Entier Naturel ?
La voie la plus simple pour répondre à la question est de dire que par définition 0 est ou n'est pas un entier naturel. En mathématiques, il est possible de poser la définition que l'on souhaite. Celle-ci se trouve marquée dans le marbre et interdit toute négociation possible. Considérons par exemple la construction de l'ensemble des entiers naturels de façon axiomatique. Le premier axiome dit que 0 appartient à cet ensemble. 0 sera ensuite défini comme le plus petit élément de cet ensemble par un axiome suivant.
L'ambiguité sur la présence du zéro dans l'ensemble des entiers naturels est abordée très clairement dans l'article de Wikipédia sur le sujet:
Au début :
En mathématiques, un entier naturel est un nombre positif (ou nul) permettant fondamentalement de dénombrer des objets comptant chacun pour un. Un tel nombre entier peut s'écrire avec une suite finie de chiffres en notation décimale positionnelle, sans signe et sans partie fractionnaire, c'est-à-dire sans chiffre « après la virgule ».
Les entiers naturels sont donc, outre zéro, ceux que l'on commence à énumérer avec la comptine numérique : un, deux, trois, quatre…
Au milieu :
Pour lever l'ambiguïté au sujet de la prise en compte de zéro comme entier naturel, l'ensemble est parfois noté « N0 ». L'indice 1 dénote alors au contraire l'exclusion de zéro. Mais l'usage consacre plus souvent pour cette restriction l'ajout d'un astérisque en exposant.
N 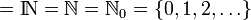
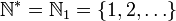
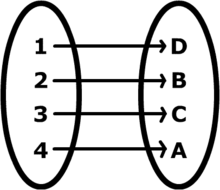
De nombreux réflexes apparaissent avec cette correspondance "nombre" à "élément" qui permet par exemple de se représenter les grands nombres, c'est la notion d'ordre de grandeur. Dans les livres de science ou d'une façon plus générale, dans les médias, on présente un ensemble comme ayant le même ordre de grandeur qu'un autre. Cela permet de se faire une image mentale de la quantité d'éléments de l'ensemble. Par exemple, j'ai à peu près autant de cheveux sur la tête qu'il y a d'Orléanais... (je sais ce n'est pas un bon exemple... allez je vous aide en donnant un indice avec le nombre attribué au dernier de mes cheveux: 113 000 ).
L'étape suivante est donc d'utiliser ces étiquettes comme standards pour des ensembles équipotents. 5 devient donc un mot pour dire qu'un ensemble possède autant d'éléments que ma main comporte de doigts.
Les langues ont différents usages pour dénombrer. Par exemple, en anglais on trouve "one man" et "a man", "a" n'étant pas considéré comme un nombre alors qu'il en a le sens. En français, on ne distingue pas "un homme" de "un homme", où les deux "un" correspondent d'une part au nombre et d'autre part à l'article. Dans certaines langues les nombres s'accordent en genre.
L'ensemble vide (par exemple la pièce qui ne contient personne ou zéro personne) est associé au nombre zéro. Là aussi on trouve des usages assez particulier comme en langue anglaise dans laquelle on trouve le singulier "one man", le pluriel "two men" et puisque "zero" n'est pas singulier, il est pluriel "zero men"! On voit donc au travers de ce simple exemple que "zéro" est loin d'avoir été naturellement intégré dans les langues comme nombre cardinal.
L'émergence du concept du zéro a été très longue. Les premières traces de cette idée sont certainement une colonne vide sur un abaque de Chine antique. Beaucoup plus tard un symbole a été utilisé en Inde à la place de ce vide.
Les nombres ordinaux
Lorsque les enfants commencent à compter, ils ne distinguent pas les nombres cardinaux (1,2,3...) des nombres ordinaux (1er, 2ème, 3ème...). La distinction se développe progressivement sans d'ailleurs qu'ils apprennnent jamais vraiment à faire la différence. Là encore la langue anglaise est un parfait exemple puisqu'elle a conservé la numération ordinale pour les dates " 5th February 2011" qui se réfère au 5ème jour du mois nommé février, à ne d'ailleurs pas confondre au 5ème mois qui serait appelé février. En français on utilise une date qui serait un peu plus cardinale " 5 février 2011" sous-entendu 5 jours écoulés depuis le début du mois.
La notion de nombre ordinal est associée en mathématiques à celle d'ensemble bien ordonné. C'est justement celà qu'avait découvert Cantor, dont nous avons parlé précédemment. Dans un ensemble bien ordonné on peut classer toutes les parties non vides possède un plus petit élément. Par exemple l'ensemble {1,2,8} est bien ordonné car chacune de ses parties {1},{2},{8},{1,2},{1,8},{2,8},{1,2,8} possède un plus petit élément.
Nous parvenons de plus à étiqueter chacun des éléments d'un ensemble bien ordonné par un nombre entier 1 puis 2 puis 3, le dernier nombre atteint correspondant à la cardinalité de l'ensemble. Il y a donc une correspondance entre la cardinalité et l'ordinalité. Le nom des étiquettes (cardinal) correspond en fait à la position de l'élément dans la liste ordonnée (ordinal). Presque tous les noms des nombres ordinaux sont d'ailleurs dérivés de ceux des cardinaux sauf dans le cas de "premier" et si nous avons "deuxième" en français, il n'en est pas de même en anglais où l'on ne trouve que "second". Sinon pour tous les suivants, il y a une correspondance exacte entre les deux types de nombres. Ceci indique que la distinction entre ordinaux et cardinaux est un concept plus récent que les nombre cardinaux eux-même. On voit bien de plus qu'il n'existe pas de mot du type "0ème" ou "0th".
Avec l'expérience, nous apprenons que compter amène au même nombre indépendant du fait qu'un bon ordre soit choisi. Il n'y a que les mathématiciens qui prennent conscience qu'il est nécessaire d'apporter une démonstration permettant de faire le lien entre ordinal et ensemble bien ordonné. Pour les ensembles infinis, l'idée du comptage et du classement s'écroule. La première idée qui serait d'utiliser les mêmes noms pour les nombres ordinaux et cardinaux, ne convient pas pour les ensembles infinis. Le problème est que nous ne savons pas si les cardinaux sont totalement ordonnés. Il n'y a qu'en acceptant l'axiome du choix que nous pouvons affirmer que deux cardinaux sont compatibles (c'est à dire qu'il existe un moyen univoque de choisir un élément d'un ensemble plutôt qu'un autre, il est donc théoriquement possible de comparer les cardinaux de deux ensembles infinis). Un autre problème est que nous ne connaissons pas quel est le cardinal suivant celui de l'ensemble des entiers naturels car cette question est équivalente à l'hypothèse du continu (c'est à dire de savoir s'il existe ou pas un cardinal entre celui des nombres entiers ou des fractions de nombres entiers -c'est le même - et celui des nombres réels). Ainsi, utiliser les nombres cardinaux comme noms d'ordinaux aboutirait à de sérieuses restrictions dans les fondements des mathématiques car l'ajout de l'axiome du choix, de l'hypothèse du continu ou leur négation aurait des conséquences non triviales. Ceci montre que les nombres ordinaux et cardinaux sont deux types d'objets différents et qu'il n'y a pas de raison, de réutiliser les nombres cardinaux comme étiquettes des nombres ordinaux, hormis dans le cas où c'est pertinent.
Il est à noter que les gens utilisent souvent des noms comme étiquettes des ordinaux comme dans l'ensemble {or,argent,bronze} pour les trois meilleurs compétiteurs. On peut aussi regarder l'ensemble des entiers relatifs: ...,-2,-1,0,1,2,... Si choisir 0 comme point de départ du comptage à droite et à gauche paraît naturel et simple, et fait coïncider l'ordinal et le nombre lui même, 1 est le premier nombre à droite de 0, -1 est le premier nombre à gauche, cette référence 0 est arbitraire. On aurait tout aussi bien pu choisir 8 comme référence et ainsi 9 aurait été le premier nombre après 8, ce qui revient à ne plus pouvoir associer les ordinaux aux nombres. Les spins des particules sont définis par des nombres tels que 0,1/2,1,3/2,... De tels noms utilisés pour des situations spéciales ne disent rien sur que devrait être un étiquetage par défaut associé à l'ordre. Il n'y a évidemment rien de faux à utiliser d'autres ensembles que celui des nombres ordinaux comme étiquettes mais s'il en est ainsi, nous devons savoir ce qu'est exactement l'ensemble des nombres ordinaux. Un mot tel que "0ème" est parfois utilisé mais cela indique une image eronnée de ce que sont les nombres ordinaux. En faisant ainsi, on utilise simplement le nom des éléments d'un ensemble bien ordonné pour étiqueter les éléments d'un autre ensemble bien ordonné.
Un peu d'ordre
Il y a deux façons d'associer un ensemble bien ordonné à chaque élément d'un ensemble bien ordonné A. Par exemple prenons A={0,2,5}.
Le premier est de définir pour chaque élément de A l'ensemble :
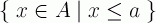
Le deuxième est de définir pour chaque élément de A l'ensemble :
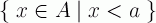
Si l'on utilise la première convention, il n'existe aucun élément associé à l'ensemble vide. Il y a au minimum un élément dans chaque ensemble même lorsque a=0. Si l'on prend la deuxième convention, il y a bien 0 qui est associé à l'ensemble vide mais aucun élément n'est associé à l'ensemble A entier, a valant au maximum 5. Le problème est qu'un ensemble bien ordonné qui possède n éléments comporte aussi n+1 "sections" et il n'y a aucun moyen de le contourner: