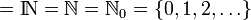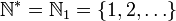O est-il un Entier Naturel ?
La voie la plus simple pour répondre à la question est de dire que par définition 0 est ou n'est pas un entier naturel. En mathématiques, il est possible de poser la définition que l'on souhaite. Celle-ci se trouve marquée dans le marbre et interdit toute négociation possible. Considérons par exemple la construction de l'ensemble des entiers naturels de façon axiomatique. Le premier axiome dit que 0 appartient à cet ensemble. 0 sera ensuite défini comme le plus petit élément de cet ensemble par un axiome suivant.
L'ambiguité sur la présence du zéro dans l'ensemble des entiers naturels est abordée très clairement dans l'article de Wikipédia sur le sujet:
Au début :
En mathématiques, un entier naturel est un nombre positif (ou nul) permettant fondamentalement de dénombrer des objets comptant chacun pour un. Un tel nombre entier peut s'écrire avec une suite finie de chiffres en notation décimale positionnelle, sans signe et sans partie fractionnaire, c'est-à-dire sans chiffre « après la virgule ».
Les entiers naturels sont donc, outre zéro, ceux que l'on commence à énumérer avec la comptine numérique : un, deux, trois, quatre…
Au milieu :
Pour lever l'ambiguïté au sujet de la prise en compte de zéro comme entier naturel, l'ensemble est parfois noté « N0 ». L'indice 1 dénote alors au contraire l'exclusion de zéro. Mais l'usage consacre plus souvent pour cette restriction l'ajout d'un astérisque en exposant.
N