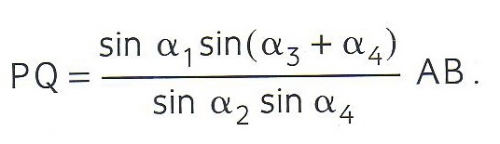Je ne suis pas un grand fan de ce que l'on appelle la situation-problème en pédagogie, car je pense qu'elle ne coïncide pas avec la façon dont on apprend et structure des connaissances et au passage on construit des compétences. Je pense que c'est une phase finale et non initiale, et qu'elle n'est pas englobante dans l'établissement des apprentissages, c'est à dire qu'elle n'épuise pas à elle seule, les mécanismes d'apprentissage intervenant dans la fixation des connaissances et l'émergence des compétences visées.
Mais pour la circonstance, je vais en proposer une, non pas pour les élèves, mais pour les enseignants de mathématiques.
Il est 6h30 du matin. Delambre et Méchain attendent patiemment sur le parvis de la Cathédrale de Dunkerque pour débuter la mesure de l'arc de méridienne jusqu'à Barcelone.
Vers 8h00, les élèves de première S1 attendront avec impatience la correction de leur exercice sur la triangulation permettant de calculer la distance PQ en fonction de la distance AB et des quatre angles codés sur la figure suivante:
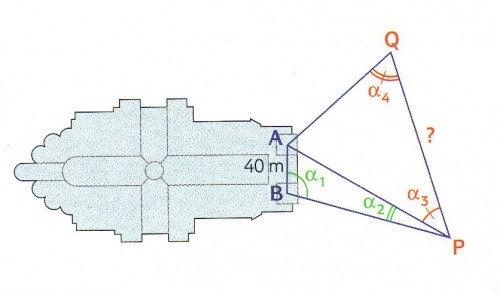
par la formule :
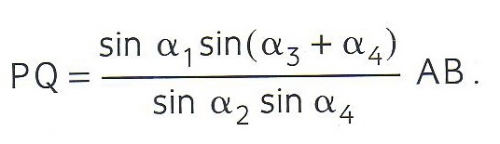
La veille le professeur de mathématiques de la classe de première S1, a oublié la réunion sur le voyage en Allemagne du petit dernier, ce qui lui a amputé toute la soirée. Il doit donc préparer en urgence, le matin, son cours. Il comprendra une animation dynamique GeoGebra du problème posé, la correction de l'exercice mais aussi la présentation de la mesure concrète et simplifiée d'une grande longueur comme cela pouvait être le cas, lors des travaux de Delambre et Méchain. Il disposera de son ordinateur portable et d'un vidéo-projecteur mais pas de connection à Internet.
Le professeur a-t-il la possibilité de réaliser son objectif, sachant qu'il a 30 mns de trajet pour rejoindre son lieu de travail?