Mathématiques et Kernésis : Une Ontologie des Formes comme Attracteurs Dynamiques

En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies. Ces derniers assurent le bon fonctionnement de nos services. En savoir plus.

Introduction au Nombre Dérivé
Contexte : Une classe de lycée où l’enseignant veut introduire la notion de nombre dérivé en évitant qu’elle soit perçue comme une simple définition formelle. L’objectif est de faire émerger la nécessité du concept avant de le formaliser, en suivant une démarche progressive, intuitive et expérientielle.
1. Identifier les attachements et résistances
L’enseignant commence par sonder les élèves sur leur rapport aux variations et aux changements.
Il pose des questions ouvertes :
• « Pouvez-vous me donner un exemple d’un phénomène qui change constamment ? »
• « Comment décririez-vous le mouvement d’une voiture ? À quel moment change-t-elle de vitesse ? »
• « Avez-vous déjà essayé de courir en accélérant progressivement ? Comment sentez-vous ce changement ? »
Les élèves évoquent des exemples variés : la vitesse d’un coureur, la fonte des glaces, l’évolution des prix.
Puis, il provoque une réaction :
« Imaginez que je vous demande de décrire précisément un changement de vitesse à un instant précis. Comment feriez-vous ? »
Les élèves tentent de répondre mais se rendent compte qu’ils ont besoin d’un outil plus précis.
Objectif : Créer un manque, une frustration productive. Ils sentent que leur langage mathématique actuel n’est pas suffisant.
2. Poser les bases de l’analyse rigoureuse
L’enseignant introduit alors une question plus formelle :
• « Si une voiture passe de 50 km/h à 70 km/h en 10 secondes, on peut calculer sa vitesse moyenne… Mais peut-on dire quelle est sa vitesse exacte au bout de 5 secondes ? »
Il guide les élèves pour analyser la situation :
• Différence entre une moyenne et une valeur instantanée.
• Distinction entre observation globale et observation locale.
Il introduit le concept de taux de variation moyen, tout en montrant ses limites : « Plus l’intervalle est petit, plus on se rapproche d’une valeur instantanée… Mais peut-on vraiment la trouver ? »
Objectif : Pousser les élèves à sentir l’importance d’une mesure plus fine du changement.
3. Explorer la notion de variation infinitésimale
L’enseignant change d’approche et propose une expérience visuelle.
• Il projette ou dessine un graphique représentant une fonction, par exemple la position d’un coureur en fonction du temps.
• Il demande aux élèves de tracer deux points proches et de calculer la pente de la sécante.
• Puis il leur fait répéter l’opération en rapprochant de plus en plus les points.
Les élèves constatent que la pente semble se stabiliser vers une valeur particulière.
L’enseignant introduit alors une métaphore :
« Imaginez que vous êtes un skieur sur une montagne. Si vous regardez de loin, la pente semble uniforme. Mais si vous zoomez au maximum, au point de voir juste sous vos skis, comment percevez-vous la pente ? »
Objectif : Faire émerger intuitivement l’idée que lorsqu’on regarde à une échelle infinitésimale, on perçoit une pente locale bien définie.
4. Laisser émerger l’intuition du nombre dérivé
L’enseignant demande alors :
• « Et si on allait jusqu’à considérer une différence infiniment petite ? Quelle valeur obtiendrions-nous ? »
Sans donner immédiatement la définition, il laisse les élèves formuler des hypothèses :
• « La pente devient unique ? »
• « Ça ressemble à une vitesse instantanée… »
Puis il introduit progressivement la notation :
• « On appelle cette valeur la dérivée d’une fonction en un point. Elle mesure la vitesse de variation à un instant précis. »
Il insiste sur le fait que cette notion est naturelle : c’est simplement une formalisation de ce que nous percevons dans la vie réelle.
Objectif : Faire ressentir le concept avant d’en donner la définition stricte.
5. Appliquer la notion à des situations concrètes
Les élèves appliquent alors cette idée à différents contextes :
• Physique : vitesse instantanée d’un objet en chute libre.
• Économie : évolution du prix d’un produit.
• Biologie : rythme de croissance d’une population.
Ils calculent les taux de variation moyens puis s’entraînent à estimer une valeur dérivée par approximation.
Puis, seulement après cette exploration, l’enseignant donne la définition formelle :
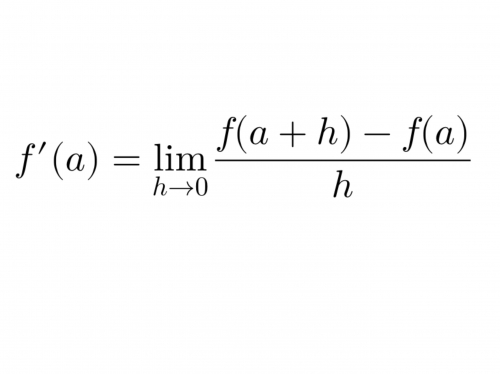
Les élèves voient alors cette expression non pas comme une formule abstraite, mais comme la concrétisation de leur propre réflexion.
Objectif : Rendre la notion incarnée, ancrée dans le réel.
6. Intégrer le concept dans une compréhension durable
Pour finir, l’enseignant ne veut pas que le concept soit oublié après le contrôle. Il invite les élèves à une réflexion plus large :
• « Où retrouve-t-on ce principe dans d’autres domaines que les sciences ? »
• « Comment cette notion pourrait-elle changer votre façon d’analyser des phénomènes du quotidien ? »
• « Peut-on imaginer une situation où la dérivée serait un concept limitant, et où une autre approche serait plus pertinente ? »
Enfin, il propose un défi pour la semaine :
« Trouvez un exemple de votre quotidien où une variation instantanée est plus importante qu’une variation moyenne, et venez en discuter au prochain cours. »
Objectif : Inscrire la notion dans une dynamique de réflexion à long terme, plutôt que de la réduire à une simple technique de calcul.
Pourquoi cette approche est puissante ?
1. Elle part de l’expérience des élèves pour introduire la nécessité du concept.
2. Elle ne donne pas la définition immédiatement mais la fait émerger progressivement.
3. Elle équilibre intuition et rigueur en passant par des images et des expériences avant d’arriver aux formules.
4. Elle inscrit l’apprentissage dans un contexte plus large, évitant que la dérivée soit perçue comme un outil froid et abstrait.
En suivant cette approche, les élèves ne « subissent » pas la dérivée, ils la découvrent et la comprennent comme une réponse naturelle à une question qu’ils se sont eux-mêmes posée.
La résolution d'un problème intéressant par Edith Kosmanek : Un quadriréacteur est-il plus sûr qu'un biréacteur ?