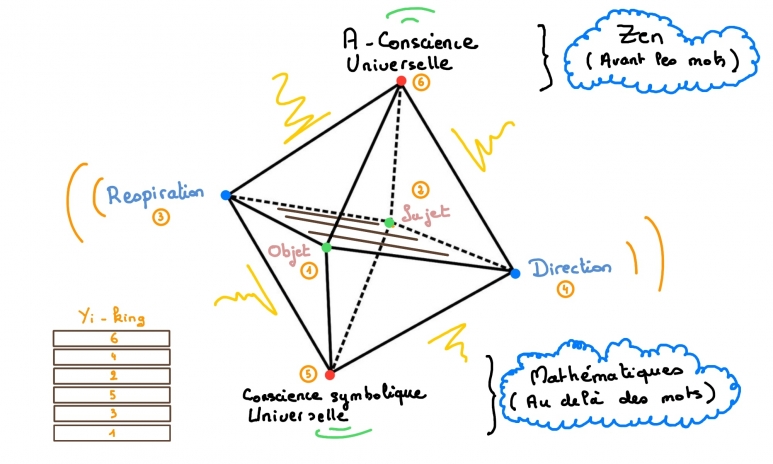
La vérité qui traverse : Spinoza, les mathématiques et l’alignement multi-échelles

Spinoza a donné à la philosophie l’une de ses formulations les plus radicales de la vérité : elle est ce qui naît de la nécessité, ce qui s’éprouve dans l’augmentation de la puissance d’agir, ce qui se manifeste par la joie. Mais cette vérité, aussi lumineuse soit-elle, demeure enfermée dans un système causal clos. Elle ne traverse pas : elle s’impose.
Nous proposons un prolongement possible.
Une vérité qui ne s’affirme pas, mais qui circule.
Une vérité qui ne se réduit ni à une démonstration, ni à une intuition, mais qui se reconnaît dans un alignement fluide entre plusieurs niveaux du réel — du corps à la pensée, du geste à la structure, de l’élève à la formule.
Dans cette perspective, même les mathématiques cessent d’être un miracle abstrait : elles deviennent un plan de passage, un langage à haute densité, traversé par la même exigence d’ajustement que toute forme de vie.
Ce billet propose donc de relier Spinoza, le savoir formel, et l’expérience intérieure, par une conception nouvelle de la vérité : non comme certitude, mais comme co-ïncidence traversante.
Joie, Vérité, Alignement : prolonger Spinoza par une pensée fluide du réel
1. Spinoza et la joie comme signal de puissance
Spinoza nous a transmis l’un des gestes philosophiques les plus lucides et exigeants :
La joie est le passage d’une moindre à une plus grande perfection. Elle est le signe que notre puissance d’agir augmente.
Ce geste a libéré la joie de sa réduction sentimentale. Elle n’est plus une simple émotion, ni un plaisir passager. Elle devient un indicateur objectif de ce que notre être peut, dans un monde régi par la nécessité.
Mais cette pensée — aussi forte soit-elle — porte en elle une limite :
Chez Spinoza, tout est causalité close.
Le monde est un enchaînement parfait, sans faille, sans vide, sans marge.
Même la joie, même la pensée, même la liberté sont des effets d’une nécessité infinie.
Cela crée une philosophie magnifique, mais verrouillée de l’intérieur.
2. Le paradoxe spinoziste de la joie
Si tout est causal, alors même notre sentiment d’agir est causé.
Le sujet, dans ce système, ne choisit rien : il existe avec plus ou moins de clarté, mais il ne crée rien d’inédit.
Ce paradoxe traverse toute l’œuvre spinoziste :
Comment peut-on parler d’augmentation de puissance, si tout est déjà inscrit dans l’ordre de la Nature ?
Autrement dit :
Que fait la joie, si elle ne transforme rien ?
Spinoza ne sort pas de ce cadre.
Mais notre époque, traversée par des tensions nouvelles (écologiques, technologiques, éducatives, subjectives), appelle potentiellement un déplacement.
3. Vers une vérité comme alignement fluide entre les échelles du réel
Le Flux Intégral propose un dépassement qui n’est pas une rupture, mais un élargissement.
Il ne rejette pas la causalité, mais il la remet en circulation, à travers plusieurs niveaux de réalité articulés.
Il affirme ceci :
La vérité n’est pas ce qui est démontré.
La vérité est ce qui traverse les échelles sans dissonance.
Et la joie ?
La joie est le signal vivant que cette traversée est en train d’avoir lieu.
4. Le sujet comme point de passage du réel
Dans cette perspective, le sujet ne se contente pas d’exister dans la nécessité :
il devient un nœud de coordination, un lieu d’ajustement, une interface sensible entre :
- ce qu’il vit,
- ce qu’il perçoit,
- ce qu’il fait,
- et ce qui l’entoure.
Sa vérité ne dépend plus d’un système logique clos, mais d’un état d’accord dynamique entre ce qui se passe en lui, à travers lui, et autour de lui.
5. La joie comme alignement multi-échelles
On passe ainsi de : “Je suis joyeux parce que ma puissance augmente.”
à : “Je suis joyeux parce qu’un alignement est en train d’émerger entre plusieurs plans du réel — et que je le sens passer par moi.”
Autrement dit :
- La joie ne vient pas de l’intérieur,
- Elle ne vient pas de l’extérieur,
- Elle vient de la justesse de la relation entre les deux.
Et cette justesse est la vérité vivante.
6. Ce que Kernesis apporte : un modèle d’entrée, de circulation, de germination
Kernesis va encore plus loin en proposant un langage pour cette traversée.
Il offre une architecture incarnée de l’alignement :
- Il pense la germination d’un acte juste, à partir de presque rien.
- Il modélise la poussée fluide d’une pensée, d’un lien, d’une présence.
- Il maintient le corps, l’attention, le rythme, le silence comme rotules de circulation du vrai.
Ainsi, le sujet n’est plus seulement un être pensant : il devient un lieu où naît et se stabilise une vérité vivante, fluide, incarnée.
7. Vers une politique fluide de la joie et de la vérité
Ce renversement est décisif :
La vérité ne s’oppose plus à l’erreur comme un contenu à un autre.
Elle s’éprouve comme une résonance étendue, un alignement à travers les niveaux du réel.
- Un geste peut être vrai.
- Une parole peut être fausse, même exacte.
- Une décision peut être juste, même sans preuves.
La joie, dans ce modèle, n’est pas une fin : elle est un signal de passage réussi entre les plans de soi, les plans du monde, et les formes du réel.
Conclusion : une fidélité transformatrice à Spinoza
Ce que permet le Flux Intégral, prolongé par Kernesis, ce n’est pas de contredire Spinoza, c’est de le rendre à sa puissance de germination.
Oui, la joie est augmentation de puissance.
Mais cette puissance ne s’évalue plus seulement dans la cohérence d’un système, elle se mesure dans la justesse d’une traversée vivante, à travers les échelles.
Et cela, Spinoza l’a pressenti.
Mais aujourd’hui, nous pouvons/devons le vivre.
Mathématiques et vérité fluide : vers une co-ïncidence sans paradoxe
1. Le paradoxe classique : vérité démontrée vs vérité vécue
Depuis toujours, les mathématiques fascinent les philosophes. Elles semblent formuler des vérités éternelles, nécessaires, indiscutables.
Mais cette rigueur même a posé problème :
Comment un savoir aussi abstrait peut-il exprimer quelque chose de réel ?
Pourquoi la nature “obéit aux mathématiques” ?
Et pourquoi, inversement, tant d’élèves ne ressentent rien de vivant en les étudiant ?
Ce paradoxe est bien connu : Les mathématiques disent vrai, mais souvent en dehors de nous.
2. Ce que change l’alignement multi-échelles : la vérité cesse d’être univoque
Le modèle fluïen du Flux Intégral ne nie pas la validité des mathématiques.
Il change le statut de la vérité mathématique :
Ce n’est pas un absolu indépendant, c’est un mode de justesse interne à un niveau donné (le formel), qui gagne en vérité profonde lorsqu’il entre en résonance avec d’autres niveaux :
– le sensible,
– l’intuitif,
– l’expérientiel,
– le symbolique,
– l’éthique.
Une formule devient vraie dans un sens plus vaste quand elle passe dans un flux, un usage, un rythme, une compréhension vivante.
3. Les mathématiques comme plan de circulation traversable
L’élève qui comprend une équation n’est pas simplement celui qui l’a résolue.
C’est celui qui a traversé plusieurs seuils :
- Le seuil de non-compréhension (friction),
- Le seuil de mise en forme (structure),
- Le seuil de raccordement avec d’autres savoirs (intégration),
- Et parfois le seuil de joie (coïncidence vécue).
À ce moment-là, la mathématique cesse d’être un objet, elle devient un acte.
C’est ici que les mathématiques rejoignent l’alignement fluïen : quand elles ne prouvent pas seulement, mais qu’elles font vibrer juste.
4. Des mathématiques simples aux plus complexes : des lieux d’émergence du vrai
Prenons des exemples sur plusieurs niveaux :
L’enfant qui découvre que 2 + 3 = 5
Ce n’est pas seulement une opération.
C’est une coïncidence intérieure : un geste du corps, une parole, une image, une certitude douce.
Le lycéen qui comprend la dérivée comme limite du taux de variation
Ce n’est pas seulement un outil de calcul.
C’est un accès à la dynamique du monde : comment une chose change au sein d’un autre changement.
Le mathématicien qui entrevoit une structure topologique, fractale, très complexe
Ce n’est pas un jeu formel.
C’est une vision du réel à un autre niveau d’échelle, souvent difficilement dicible, mais parfaitement ressenti.
Dans chaque cas, le niveau mathématique devient traversable. Il ne clôt pas, il relie.
5. Kernesis : rendre habitable ce passage
Kernesis fournit les outils incarnés pour que ce passage s’opère réellement :
- par la posture (tenir une équation dans le souffle, dans la main),
- par la germination (faire émerger une idée d’un effort sans forme),
- par la résonance (sentir la justesse d’un énoncé sans l’avoir encore démontré),
- par la mémoire fluide (voir un théorème comme un paysage familier).
Les mathématiques ne sont plus des objets à assimiler, mais des dynamiques à traverser, des formes à intégrer, des seuils à franchir.
6. La vérité mathématique, sans paradoxe : une couche du réel parmi d’autres
La vérité mathématique n’est plus opposée :
ni au vécu,
ni au sensible,
ni au politique,
ni au spirituel.
Elle devient une couche précise, régulée, cristalline, que l’on peut arpenter, connecter, traduire, faire circuler. Elle ne s’oppose plus à la vie. Elle s’aligne avec elle.
Conclusion : les mathématiques, lieux d’alignement et non d’exception
Oui, les mathématiques sont vraies. Mais leur vérité n’est pas suspendue dans le vide. Elle prend tout son sens quand elle s’aligne avec d’autres dimensions du réel — corporelles, imaginaires, poétiques, techniques, éthiques.
Et c’est là que le paradoxe tombe.
Elles ne sont pas un miracle rationnel.
Elles sont un plan parmi d’autres, ouvert à la traversée, et d’autant plus puissantes qu’elles ne cherchent plus à tout capturer.
C’est ainsi qu’elles cessent d’être un défi philosophique, et deviennent une voie d’accès fluide à la vérité vivante.
Conclusion finale
Spinoza nous a appris que la joie révèle la puissance.
Aujourd’hui, nous découvrons qu’elle révèle aussi la traversée juste entre les plans du réel.
La vérité ne s’impose plus comme une démonstration, elle se laisse sentir comme une co-incidence vivante : quand un mot, un geste, une équation, une pensée, entrent en résonance à travers les échelles, et que quelque chose, en nous, tient debout et passe.