SpaceTime:un logiciel de calcul scientifique
Je viens de découvrir SpaceTime, un logiciel de calcul formel, de représentation et plus généralement de calcul scientifique. Il est très fluide et libre! Il me semble de plus excellent pour le peu que j'en ai testé. Il suffit de cliquer sur les graphiques pour les agrandir puis de recliquer sur la fenêtre pour revenir au CAS.
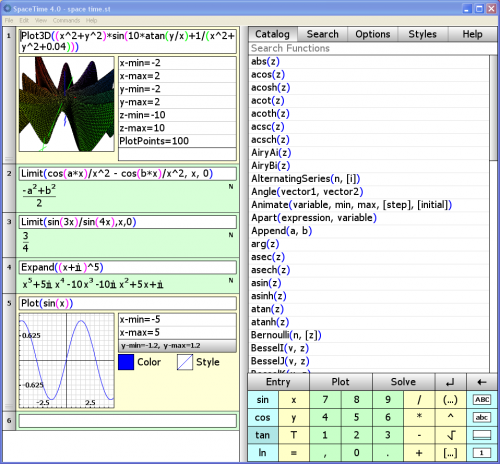
Voilà une copie d'une fenêtre que j'ai réalisée, avec la représentation d'une surface, d'une courbe, le développement d'un binôme avec une valeur complexe et deux calculs de limites:
Un essai de représentation dans l'espace avec le code associé:
MultiPlot3D(Plot3D((y-4,x-2),[x,-10,10],[y,-10,10],colors=[orange,blue]),ParametricPlot3D((u,v,500),[u,-1000,1000],[v,-1000,1000],color=[green]),Plot3D((0.001*(x^2+y^2)),color=[yellow]))
J'ai quelque peu "bidouillé" pour obtenir un affichage cohérent entre les deux plans y=4 et x=2 et le plan horizontal qui nécessite une définition paramétrique.
Une courte vidéo permettant de voir le basculement entre les fenêtres de visualisation et le CAS:
La vidéo de présentation:
A ne pas oublier: le blog sur lequel j'ai découvert ce logiciel.