Depuis qu'est né le livre scolaire de mathématiques au début du XVIIIème siècle, celui-ci n'a cessé d'évoluer pour prendre des formes différentes et répondre à des objectifs variés en fonction des besoins personnels ainsi que des politiques en vigueur. Des noms célèbres tels que par exemple, Clairaut ou Bézout, y ont apporté leur contribution et justifié leur démarche en les inscrivant dans les priorités du moment.

Les temps ont changé. De nouveaux environnements, en particulier numériques, sont apparus, mais les besoins principaux sont toujours exprimés dans des termes très similaires: permettre à l'élève de parcourir une partie des mathématiques, en ne s'y perdant pas,  si possible de façon autonome et en augmentant ses compétences.

Ce sont ces objectifs que s'est fixé Frédéric Laroche en publiant un ouvrage papier, l'inscrivant ainsi dans une certaine tradition, adapté aux récents programmes de seconde, introduisant l'usage d'outils logiciels et la pratique de l'algorithmique, de la logique, tout  en faisant référence aux tests internationaux. Il tire aussi bénéfice de la publication en ligne (principalement pour les corrections et les fiches vierges de restitution du cours. Le livre prend plus la forme d'un cahier d'activités que d'un livre de cours. L'élève peut d'ailleurs,  au moins partiellement, y placer des éléments de réponses. Les cinq parties formant l'essentiel du corpus de la classe de seconde (fonctions affines/droites, géométrie, calculs, fonctions, probabilités et statistiques) sont construits sur le même schéma pédagogique:

• Une fiche vierge permettant d'y reporter les éléments principaux à connaître. Le cours n'est pas fourni mais il est demandé à l'élève d'en retrouver l'essentiel.

• Des applications directes du cours.

• Des exercices intermédiaires.

• Des exercices avec prise d'initiative, pour réfléchir et aller plus loin.

On retrouvera ces 3 "moments" pédagogiques incontournables: les processus de base, les méthodes et la résolution de problèmes, dans le document "Apprendre à apprendre" que j'ai publié. 

Le reste du cahier est composé:

• de la  partie "Algorithmique et calculatrice" qui permet de mettre "en pratique" les mathématiques.

• de références aux test internationaux avec des énoncés en langue anglaise.

• de la partie "Pourcentages, problèmes et raisonnement" qui permet de faire un tour d'horizon avec des difficultés variées.

• d'une partie logique qui permet de travailler ce domaine délicat qui s'est absenté pendant de nombreuses années des priorités scolaires.

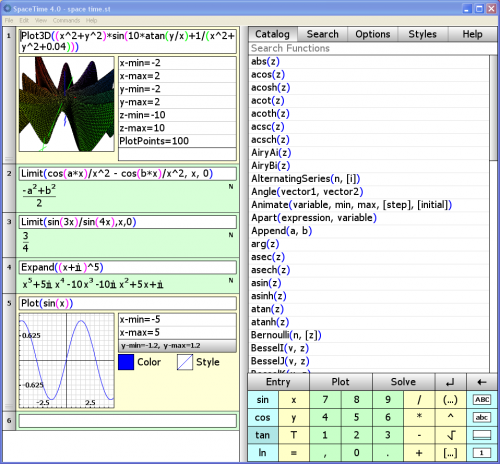
• de la dernière partie qui est consacrée à des activités nécessitant le logiciel GeoGebra.

Je tiens aussi à signaler que le cahier n'est pas dénué d'humour comme en témoignent les dessins de Florence Bleuse.

On trouvera ICI un extrait du cahier d'activités et les corrections des exercices à cette page.

Pour savoir si vous êtes en forme, je vous propose un petit problème de robinets que l'on trouvera page 97:

Lorsque je fais couler l'eau chaude je mets 30 mns pour remplir la baignoire. Lorsque je fais couler l'eau froide je mets 20 mns. Combien de temps mets-je avec les deux robinets ouverts simultanément?

Et je ne veux pas voir de (30+20)/2=25 mns ! Deux robinets ouverts ne mettent pas plus de temps à remplir une baignoire qu'un seul des deux.

Google Trend permet de dresser des courbes associées aux requêtes sur certains mots-clés. Inutile d'être un expert pour voir que la tendance de recherche est décroissante sur le long terme pour  "mathématiques" et "mathematics".

Le graphique précédent était en échelle relative, c'est à dire en fraction des recherches totales, mais le résultat n'est pas beaucoup plus réjouissant en échelle absolue sur la même période:

La tendance internationale suit la même pente...

Les origines des requêtes sont intéressantes à analyser, car elles ne sont pas sans surprise :

Pays:

Villes:

Langues:

La Chine n'est bien sûr pas présente dans ces statistiques puisque les requêtes se font majoritairement via Baïdu dans ce pays et non Google (le chinois est cependant la troisième langue mondiale utilisée, en dehors de la Chine!). Nous pouvons cependant remarquer que si la France est le pays des mathématiques, elle l'est peut-être en terme de médailles mais elle n'apparaît pas dans les dix premiers pays pour le nombre des requêtes et le français apparaît timidement en 9ème position pour les langues utilisées. Il est à noter l'allemand se porte plutôt bien, nous sommes derrière la Turquie et de façon assez surprenante, l'anglais n'est pas  la première des langues apparaissant dans cette analyse mais le tagalog que je ne connaissais même pas de nom!

Les Etats-Unis sont aussi les grands absents de ces données!

A méditer.

Je viens de découvrir SpaceTime, un  logiciel de calcul formel, de représentation et plus généralement de calcul scientifique. Il est très fluide et libre! Il me semble de plus excellent pour le peu que j'en ai testé. Il suffit de cliquer sur les graphiques pour les agrandir puis de recliquer sur la fenêtre pour revenir au CAS.

Voilà une copie d'une fenêtre que j'ai réalisée, avec la représentation d'une surface, d'une courbe, le développement d'un binôme avec une valeur complexe et deux calculs de limites:

Un essai de représentation dans l'espace avec le code associé:

MultiPlot3D(Plot3D((y-4,x-2),[x,-10,10],[y,-10,10],colors=[orange,blue]),ParametricPlot3D((u,v,500),[u,-1000,1000],[v,-1000,1000],color=[green]),Plot3D((0.001*(x^2+y^2)),color=[yellow]))

J'ai quelque peu "bidouillé" pour obtenir un affichage cohérent entre les deux plans y=4 et x=2 et le plan horizontal qui nécessite une définition paramétrique.

Une courte vidéo permettant de voir le basculement entre les fenêtres de visualisation et le CAS:

La vidéo de présentation:

A ne pas oublier: le blog sur lequel j'ai découvert ce logiciel.

Il y a un an et demi, j'enfilais quelques perles mathématiques sur Pearltrees presque seul. Aujourd'hui, force est de constater que la culture de la perle se porte bien et nous permet de faire une visite originale du web mathématique.

Bon voyage en cliquant sur l'image.