Des outils pour favoriser l'apprentissage du calcul numérique et littéral
Deux outils pour aider à l'apprentissage des règles de calcul littéral et de manipulation algébrique ont attiré mon attention.
Mathematical Expression Structure Tool
Mathematical Expression Structure Tool permet de visualiser toute expression numérique, littérale ou mixte à l'aide d'un arbre. Il est possible de générer les expressions avec l'affectation d'une probabilité pour chaque signe opératoire. Il est possible d'y inclure les parenthèses et les nombres négatifs. L'utilisateur peut aussi choisir sa propre expression.
Une fois l'arbre affiché, plusieurs choix sont possibles:
Explorer l'arbre
Evaluer les expressions numériques intermédiaires en pouvant aller jusqu'au résultat final.
Repérer dans l'expression ou dans l'arbre, un nombre, une variable littérale ou un signe opératoire.
EpsilonWriter
Le second outil est EpsilonWriter. Son potentiel pédagogique pour l'aide au calcul a été traité dans le Repères Irem 92. Le principe est d'associer une manipulation algébrique ou numérique au geste, celui du déplacement de la souris.
Je reviendrai très prochainement sur ce logiciel qui apporte de nouvelles dimensions à l'écriture des mathématiques. Un chat est en effet disponible ainsi que la possibilité de partage de document. Il est aussi possible d'utiliser EpsilonWriter pour éditer des mails à contenu mathématique et le code peut être exporté sur des blogs. J'ai écrit un article il y a quelque temps, publié sur Mathematice posant l'environnement numérique comme un bain dans lequel seraient plongées les trois sphères, de la pédagogie, de la didactique et de la communication. EpsilonWriter me semble bien être un des tous premiers éléments de l'intersection de ces trois sphères.
Le vidéo qui suit n'a pas pour but de montrer toutes les potentialités du logiciel mais seulement de découvrir quelques manipulations de base. Pour l'ensemble des fonctionnalités, il suffit de se diriger vers les présentations disponibles sur le site.
Les applets de l'Institut Freudenthal
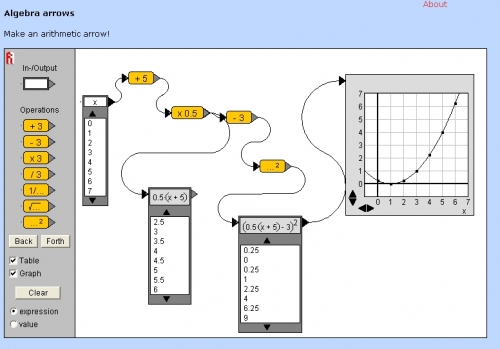
Notons aussi l'existence des excellents applets de l'Institut Freudenthal. J'avais présenté sur ce blog l'applet Algebra Arrows.