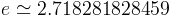Qu'est-ce que la science? Comment distinguer un argumentaire scientifique de ce qui n'en est pas un? Ou pire de ce qui ne l'est pas tout à fait? Raisonnements éronnés, glissements de sens, effets de rétorique, les techniques sont nombreuses pour nous faire avaler l'ersatz à la place du produit original. Produit d'ailleurs qui se prête bien mal à sa digestion par le grand public. Mais tous les coups sont-ils permis? Ne finit-on pas par s'habituer au packaging? Et ne reproduit-on pas, parfois malgré-nous, les biais que l'on souhaiterai éviter?

Les mathématiques ne sont pas exemptes de cette vulgarisation abusive ou de leur usage détourné. On y trouvera comme exemple, la célèbre maladie de la Gödelite, c'est à dire des conclusions des théorèmes de Gödel mises à toutes les sauces, le fameux Chaos et son effet papillon, la vision très mystique et pythagoricienne du monde, la théorie des catastrophes utilisée de façon... catastrophique et nos plus grands mathématiciens oscillant entre grandeur et décadence. Le Post-modernisme quant à lui fut friand d'un vocabulaire mathématique, dont l'utilisation est bien souvent inadaptée en même temps que le sens des concepts  sous-jacents incompris.

A l'interstice du monde scientifique qui diffuse  et du grand public, la zététique propose d'une part de lister les principales sources d'égarement et de confusion, aussi bien dans les textes que dans les titres des revues de vulgarisation. Elle offre aussi un matériau pédagogique pour s'exercer et pour traiter des cas "d'école".

Après avoir lu la thèse de Baudoin Jurdant : Les problèmes théoriques de la vulgarisation scientifique, je me suis attaqué à une  autre thèse, plus orientée vers les cas pratiques, celle de Richard Monvoisin, Pour une didactique de l'esprit critique.

Entre carpaccios et effets paillasson, le propos est intéressant et permet de disposer d'indicateurs concrets pour déceler les effets utilisés afin de valider un propos qui n'a rien de scientifique alors que son auteur le proclame ou le présente comme tel ou en fait un argument qui devrait être irréfutable.

Au fur et à mesure de la lecture, on découvre des encarts faisant apparaître une maxime intitulée "Facette Z" (comme Zététique ou Zorro?). Elle permet de synthétiser un passage incontournable pour diffuser au plus près les objets de Science. Un exemple parmi beaucoup d'autres: "Les faits, rien que les faits quelquesoit la personne qui les rapporte".

On trouvera un résumé-condensé des facettes Z dans le cours de Zététique-Méthodologie Scientifique de Broch à la page 47.

Il est intéressant de noter dans un sondage de 2001 (page 36), que "seulement" 72.3% des européens pensent que les mathématiques sont plutôt scientifique contre 92.6% pour la médecine et 52.7% pour l'astrologie!

Il est à noter aussi l'existence de l'observatoire de Zététique et de l'AFIS.

Bonne lecture.

Photo: dgj103

Personnellement ça me fait rire, je trouve même ça un peu "kitch", mais l'essentiel c'est qu'on en parle.

Le 14 mars c'est le jour consacré à Pi pour 3,14.....

Aujourd'hui le 7 février c'est le jour anniversaire de  "e" pour :

Je lis en ce moment un livre très intéressant qui est en fait la réédition de la thèse de Baudoin Jurdant intitulée "Les problèmes théoriques de la vulgarisation scientifique". Je me suis toujours demandé si la vulgarisation mathématique était vraiment possible, principalement pour répondre à la mission qu'elle se fixe implicitement, celle de développer l'image et la vision des mathématiques auprès d'un public qui n'y est pas nécessairement disposé. Il y a quelques temps, j'avais lancé un petit sondage sur l'utilité de la vulgarisation. Le questionnaire ci-après permettra peut-être de mieux cerner le sujet. N'hésitez pas à y répondre même de façon très incomplète, c'est aussi un indice de la difficulté de la vulgarisation et en particulier de la vulgarisation mathématique.

Vos réponses

tice et mathématiques