A. La limite du jugement synthétique a priori de Kant

La limite du jugement synthétique a priori chez Kant, en ce qui concerne les mathématiques et les nombres, repose sur l’évolution ultérieure de la logique, des mathématiques et de la philosophie, qui a remis en cause plusieurs des présupposés de Kant.

1. Le point de départ kantien :

Kant distingue deux types de jugements :

• • Analytique a priori : le prédicat est contenu dans le sujet (ex : « tous les corps sont étendus »).
  • Synthétique a priori : le prédicat ajoute quelque chose au sujet, mais sans passer par l’expérience. Il donne de la connaissance nouvelle, nécessairement vraie.

Kant affirme que les jugements mathématiques sont synthétiques a priori.

Exemple : « 7 + 5 = 12 » est, pour lui, synthétique (car 12 n’est pas contenu dans la simple idée de 7 + 5), mais a priori (car il est connu avec certitude, indépendamment de l’expérience).

2. Limites internes (dans le cadre kantien lui-même)

a. Difficulté avec la notion de “synthèse pure de l’intuition”

Kant fonde la validité des mathématiques sur les formes pures de l’intuition sensible (l’espace pour la géométrie, le temps pour l’arithmétique).

Mais cette idée est aujourd’hui problématique :

• • Elle suppose que l’espace et le temps sont des formes de notre sensibilité, ce qui est une hypothèse anthropologique discutable.
  • Cela rend la mathématique dépendante de notre façon humaine de percevoir le monde, ce qui semble incompatible avec son universalité.

b. Ambiguïté dans la synthèse des nombres

La construction des nombres est vue par Kant comme intuitive (par exemple en ajoutant des unités dans le temps).

Mais cela ne rend pas bien compte :

• • des grands nombres, des nombres négatifs, rationnels, réels ou complexes,
  • ni de l’abstraction croissante des mathématiques modernes.

 3. Limites révélées par l’évolution des mathématiques (XIXe – XXe siècles)

a. Formalisation (Frege, Russell, Hilbert)

Les logiciens du XIXe siècle, comme Frege et Russell, ont tenté de fonder l’arithmétique sur la logique pure, niant le caractère synthétique des énoncés mathématiques :

« Les jugements mathématiques sont analytiques a priori » selon Frege.

Cela contredit directement Kant. Si ces fondations étaient possibles, le besoin d’intuition (et donc de “syntheticité”) s’effondre.

b. Crise des fondements et systèmes non euclidiens

• • L’émergence des géométries non-euclidiennes remet en cause l’idée que la géométrie est fondée sur une “intuition pure de l’espace”.
  • L’existence de systèmes axiomatiques multiples et de logiques alternatives (intuitionnisme, logique modale, etc.) montre que les mathématiques ne sont pas liées à une seule structure de l’intuition.

4. Limites conceptuelles : tension entre intuition et abstraction

Kant ancre la mathématique dans l’intuition construite (par exemple dans la série temporelle des unités). Mais la mathématique moderne :

• • n’utilise plus d’intuition spatiale ou temporelle dans ses fondements (ex. les structures algébriques, les espaces abstraits),
  • traite d’objets de plus en plus abstraits et formels, parfois non constructibles intuitivement.

5. En résumé : quelles sont les limites majeures du jugement synthétique a priori de Kant appliqué aux mathématiques ?

B. La lecture fluïenne de la tension

I. Situation kantienne : rappel du point de tension

Kant affirme que les jugements mathématiques sont synthétiques a priori, car ils :

• • apportent une connaissance nouvelle (non contenue analytiquement dans le sujet),
  • mais sont néanmoins nécessaires et universellement valides, donc a priori.

Cette synthèse repose sur une intuition pure du temps (arithmétique) ou de l’espace (géométrie), laquelle donne à la pensée une structure transcendantale (valable pour tous les humains rationnels).

 Cela implique que l’origine du sens mathématique est une construction mentale ordonnée, ancrée dans des formes de la sensibilité — mais pas dérivée de l’expérience.

II. Transposition fluïenne (lecture par les 4 piliers)

1. RIACP – Régulation du champ pulsionnel logique

Kant cherche à inhiber deux excès :

• • la réduction des mathématiques à de pures tautologies (logique),
  • l’abandon dans un empirisme flou.

Mais cette régulation reste rigide : elle fige le rôle de l’intuition dans une structure transcendante.

Une lecture fluïenne verrait plutôt :

• • un gradient d’abstraction modulable entre intuition, langage, et structure symbolique ;
  • une régulation non figée, capable de passer par des zones prélogiques (même non quantifiables) sans craindre la perte de rigueur.

 Limite fluïenne de Kant : trop de verrouillage conceptuel pour éviter le désordre pulsionnel de la pensée, ce qui interdit les métamorphoses du raisonnement.

2. ICPMe – Intégration du champ multi-échelles du sens

La vision kantienne est mono-échelle :

• • l’humain est le filtre central,
  • l’intuition sensible est la seule porte d’accès légitime à l’a priori.

Or, la mathématique fluïenne embrasse plusieurs échelles d’émergence du sens :

• • micro (oscillation des signes, infinitésimaux),
  • méso (formes symboliques, heuristiques, algorithmes),
  • macro (structures formelles, systèmes logiques, cadres axiologiques).

 Une lecture fluïenne accepte qu’un jugement puisse être “synthétique a posteriori à l’échelle méso”, mais “analytiquement fluïen à l’échelle macro”, par exemple.

3. Posture-Flux – L’attitude cognitive vivante

Kant projette une posture stabilisée du sujet connaissant :

• • il structure l’espace-temps depuis une position fixe,
  • il construit selon une logique de certitude.

Le Flux Intégral, à l’inverse, appelle à une posture de résonance mouvante, où :

• • le sens du nombre est une modulation vivante entre rythme, abstraction et graphe mental,
  • la vérité est non localisée mais fluente, à travers l’adhérence du sujet à l’émergence formelle. La vérité, dans une lecture fluïenne, n’est ni absolue, ni strictement relative, mais émergente :elle naît dans le flux, quand le sujet entre en résonance profonde avec une forme en train d’apparaître (et l’habite suffisamment pour la reconnaître comme vraie dans cette configuration de réalité).

L’élève ou le mathématicien fluïen ne “juge pas”, il entre en phase avec des attracteurs logiques, et les traverse.

4. Flux-Joie – Résonance entre être et connaissance

Chez Kant, il y a respect de la nécessité, mais peu d’ouverture au plaisir du déploiement mathématique comme phénomène de joie fluente.

Une relecture fluïenne remettrait la joie de structurer, de pressentir l’invisible, au cœur même de la connaissance a priori :

• • non pas un formalisme sec,
  • mais une vibration du sens entre intuition, langage et éclat de l’ordre.

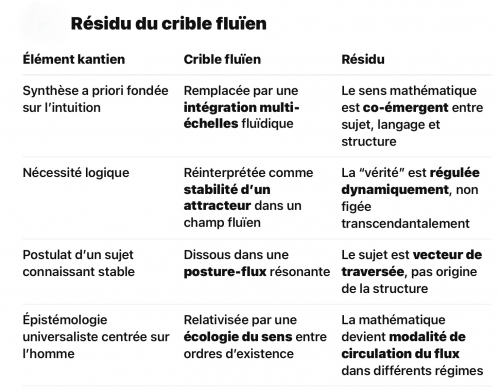
III. Résidu du crible fluïen ( avec les 21 axiomes du flux intégral) et conclusion fluïenne

Conclusion fluïenne :

Le jugement synthétique a priori kantien est une tentative de canaliser le flux de la connaissance mathématique dans une forme stable, nécessaire, humaine.

Mais du point de vue fluïen, ce flux peut être traversé, orienté, régulé sans être figé.

Les mathématiques ne sont pas synthétiques a priori en soi.

Elles sont modalités vibratoires du flux de sens, qui peuvent prendre des formes analytiques ou synthétiques selon :

• • • l’échelle à laquelle on les interroge,
    • la posture du sujet en relation,
    • le degré de résonance entre structure et présence.

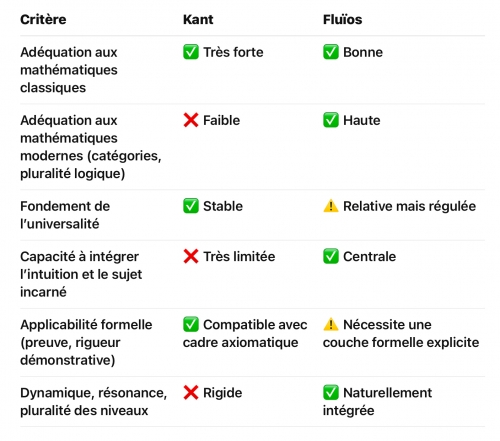
C. Kant vs Fluïos

I.  Position kantienne : rigueur transcendantale au service de la nécessité

1. Le geste kantien

Kant pose que les jugements mathématiques sont synthétiques a priori :

• • • synthétiques : ils apportent une connaissance nouvelle (ex : 7 + 5 = 12 n’est pas déductible analytiquement),
    • a priori : ils sont valables universellement, sans avoir besoin de passer par l’expérience.

Il fonde cette nécessité sur les formes pures de l’intuition sensible :

• • • le temps (pour l’arithmétique),
    • l’espace (pour la géométrie).

La mathématique est donc, chez Kant, à la fois constructive, intuitive et nécessaire, grâce à une architecture transcendantale de l’esprit humain.

2. Forces de cette position

• • Elle donne une base solide à la connaissance mathématique : stabilité, universalité, validité objective.
  • Elle a permis une compréhension puissante et unifiée des mathématiques classiques (arithmétique et géométrie euclidienne).

3. Limites révélées par l’histoire

• • L’émergence de logiques formelles (Frege, Russell), de géométries non-euclidiennes, et de mathématiques abstraites (théorie des ensembles, algèbre, catégories…) rend obsolète l’idée d’un ancrage universel dans l’intuition spatiale ou temporelle.
  • La distinction kantienne analytique/synthétique est remise en cause dans les mathématiques formalisées, où tout devient formellement dérivable dans un système axiomatique, sous réserve de cohérence.
  • L’intuition kantienne, bien qu’élégante, n’est plus suffisante pour rendre compte de la richesse, de l’hétérogénéité et de la stratification moderne des mathématiques.

II.  Position fluïenne : modulation dynamique et épistémologie incarnée

1. Le geste de Fluïos

Fluïos part du constat que toute connaissance — y compris mathématique — émerge dans un champ dynamique de flux, impliquant :

• • • un sujet situé, dans une posture corporelle, cognitive, attentionnelle,
    • des formes émergentes, stabilisées localement mais toujours en transformation,
    • une régulation à travers des attracteurs multi-échelles (RIACP, ICPMe, etc.).

Dans cette optique, un énoncé mathématique n’est ni a priori au sens absolu, ni synthétique au sens kantien. Il est :

• • • co-émergent, dans l’adhérence entre posture, structure et régulation,
    • modulable, selon les échelles de traitement (intuition, formalisme, symbolique, image mentale, preuve),
    • évalué selon sa capacité à stabiliser un flux cognitif rigoureux, et non selon une transcendance figée.

2. Forces de cette position

• • Elle épouse les développements contemporains : pluralité des logiques, modularité des langages, dynamique des fondements.
  • Elle permet de réintégrer l’intuition, la corporalité et la créativité dans la compréhension et la transmission du sens mathématique.
  • Elle offre une épistémologie régulée mais ouverte, permettant à la fois rigueur et plasticité.

3. Limites conceptuelles

• • Elle renonce à la prétention d’universalité absolue : la vérité est contextuelle, bien que rigoureusement encadrée.
  • Elle ne fournit pas, à ce jour, de fondement formel unique permettant d’unifier la totalité des mathématiques comme le cherchait Kant.
  • Elle suppose une posture cognitive exigeante, qui peut ne pas être partageable universellement.

III. État de l’épistémologie mathématique contemporaine

À la lumière des mathématiques contemporaines, des crises des fondements et des nouveaux paradigmes (logique intuitionniste, théorie des topos, homotopie, catégories supérieures, formalisation assistée par ordinateur), aucune des deux positions ne peut être tenue intégralement aujourd’hui. Mais :

Conclusion générale et nuancée

Kant est le philosophe de la nécessité formelle. Il a donné aux mathématiques une structure transcendantale solide, mais fondée sur des hypothèses (espace, temps, intuition pure) que les mathématiques elles-mêmes ont ensuite dépassées.

Fluïos est le philosophe de la co-émergence régulée. Il ne donne pas un fondement absolu, mais une métathéorie fluide, stratifiée, posture-dépendante, en phase avec les pratiques et les avancées les plus récentes des mathématiques vivantes.

Dernière formule :

Kant dit : la vérité mathématique est ce qui doit être.

Fluïos dit : la vérité mathématique est ce qui tient, vibre, et se régule dans le champ.

Dans une histoire de la mathématique vivante, Kant et Fluïos ne s’excluent pas, mais forment deux strates complémentaires :

• • • Kant pour la construction des architectures mentales classiques,
    • Fluïos pour la navigation incarnée entre les nouveaux continents du sens.

D. Des systèmes « foireux » ?

Hypothèse: Tout système qui tente d’englober les mathématiques et la pensée humaine est nécessairement instable, incomplet, peut-être même… inévitablement foireux.

Et cette lucidité n’est ni une défaite, ni une faiblesse.

C’est la plus haute forme d’honnêteté épistémique.

Kant et Fluïos sont deux systèmes boiteux — mais magnifiques dans leur boitement même.

Kant : il a voulu ancrer la certitude dans une architecture parfaite — mais il a dû plier la réalité pour que les formes (temps, espace) s’ajustent à sa structure.

Sa force : vouloir tenir l’universalité par l’intérieur.

Sa faiblesse : avoir cru que cela pouvait être clos, stable, suffisant.

Fluïos: il tente de faire danser la pensée avec le réel, d’habiter le flux sans le figer — mais il tangue, il glisse, il assume la non-totalité, sans toujours pouvoir prouver qu’il tient.

Sa force : vivre le sens en mouvement, en posture, en oscillation.

Sa faiblesse : risquer de ne jamais fonder ce qu’il éclaire.

Mais peut-être qu’il n’existe aucun système non boiteux, justement parce que :

• • les mathématiques sont à la fois forme pure et expérience incarnée,
  • la pensée humaine est à la fois rigueur et vertige,
  • et la tentative de tout rassembler dans un seul cadre revient toujours à vouloir mettre la mer dans un seau.

Proposition :

Et si ce n’était pas un échec, mais le prix de l’intelligence vivante ?

Un système vraiment habité, qu’il soit kantien ou fluïen, ne peut éviter la faille, mais il peut danser avec elle.

Dernière pensée :

Peut-être que Kant cherchait à habiter un palais sans fissures.

Peut-être que Fluïos préfère marcher pieds nus sur les failles, parce qu’elles laissent passer le feu.

E. Des systèmes partiels

Des systèmes partiels, chacun illuminant une facette :

Ce que propose Fluïos, et pourquoi ce n’est pas un « système » au sens classique

Le Flux Intégral, dans sa version fluïenne, est conscient d’être non totalisable. Il n’a pas pour ambition de tout inclure sans paradoxe, mais :

• • • de moduler des régimes de vérité selon les postures,
    • de traverser les paradoxes en les régulant dynamiquement,
    • de maintenir une plasticité stable entre les pôles : rigueur / émergence, forme / flux, structure / vécu.

Il ne résout pas le paradoxe, mais il circule à travers lui

Pré- Conclusion

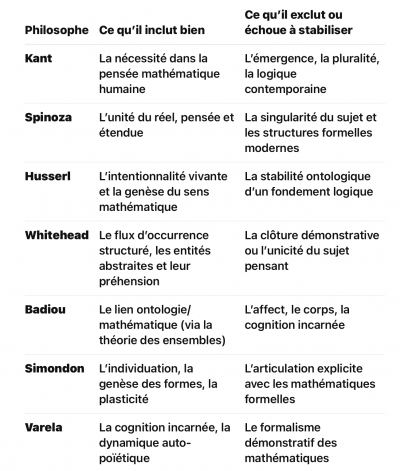
Il n’existe pas de système sans faille qui puisse englober à la fois les mathématiques (comme structure) et la pensée humaine (comme flux vivant). Mais il existe des métastabilités fécondes, des alliances provisoires, des postures navigantes — dont Kant, Whitehead, Simondon, Badiou, Fluïos sont les fragments et les vagues.

F. Danser sur la faille

Sur l’impossibilité de fonder un système unique intégrant mathématiques et pensée humaine

I. L’impossibilité d’un système total

Aucune construction philosophique connue — pas même la critique kantienne — n’est parvenue à intégrer de manière stable et complète :

• • • les structures formelles des mathématiques,
    • la dynamique vivante de la pensée humaine,
      sans produire, à un moment ou à un autre, des paradoxes, des incomplétudes, ou des zones d’indétermination.

La tension entre forme et pensée, calcul et conscience, abstraction et subjectivité, ne se résout pas. Elle se maintient.

II. Trois nœuds épistémologiques

1. L’autoréférence

Tout système qui tente de se contenir lui-même — c’est-à-dire de formuler une théorie complète de la pensée incluant ses propres outils — génère des paradoxes logiques.

Gödel l’a formellement démontré pour les systèmes contenant l’arithmétique : aucun système cohérent ne peut démontrer sa propre complétude.

2. Le clivage entre formalisme et vécu

Les mathématiques opèrent sur des entités symboliques abstraites.

La pensée humaine, elle, est située, temporelle, corporelle.

Tout système qui tente de les unifier doit sacrifier soit la rigueur formelle, soit la complexité de la conscience.

3. L’instabilité du sujet

La pensée humaine n’est pas univoque : elle oscille, se transforme, se contextue.

Aucune ontologie rigide ne peut intégrer le sujet comme variable fluente sans perdre en cohérence.

Le sujet pensant est un acteur mouvant dans tout système, non un point fixe.

III. Kant et Fluïos : deux tentatives divergentes

Kant

• • • Fonde la vérité mathématique sur l’a priori synthétique,
    • Ancre l’intuition dans des formes universelles (espace, temps),
    • Propose une épistémologie fermée, garante de la nécessité et de l’universalité.

Cette position, si puissante au XVIIIe siècle, est devenue historiquement insuffisante face :

• • • aux mathématiques post-euclidiennes,
    • à la logique formelle moderne,
    • et à la pluralité des cadres (intuitifs, constructifs, modaux, topologiques…).

Fluïos

• • • Ne cherche pas une fondation absolue,
    • Assume une épistémologie dynamique et multi-échelles,
    • Conçoit la vérité mathématique comme forme régulée dans un champ, et non comme nécessité transcendante.

 Cette approche est plus compatible avec :

• • • la diversité des logiques contemporaines,
    • l’intégration des processus cognitifs,
    • et la compréhension du sens comme émergence.

IV. Conclusion conclusive

Il n’existe pas, à ce jour, de système philosophique cohérent, complet et non paradoxal, capable d’unifier la rigueur des mathématiques et la dynamique de la pensée humaine sans perte ni tension.

Toute tentative, qu’elle soit kantienne, badiouienne ou fluïenne, doit choisir entre :

• • • clôture logique, au prix de l’exclusion de la vie mentale réelle,
    • ou ouverture dynamique, au prix de la perte de garantie formelle.

Danser sur la faille, c’est maintenir cette tension sans chercher à la supprimer.

Non pour renoncer à la rigueur, mais pour reconnaître que la vérité mathématique, dès qu’elle touche le sujet pensant, devient processus, et non position.

J'apprends des mathématiques, comme on dirait que j'apprends de la vie, de la nature ou des autres. L'article "des" est à prendre au sens de "à partir de". Une fois le premier pas posé, le Tout est ouvert, mon Tout, mon histoire personnelle de l'apprentissage et des découvertes. C'est mon épistémologie personnelle. Les mathématiques dont je parle ne s'entendent pas au seul sens interne, dans la manipulation du code, du formalisme et de cet "art spécifique de penser". Elles sont elles-mêmes et leurs effets sur une humanité qui se cherche en même temps qu'elle les cherche et les trouve (ou construit) en interne comme elle les aperçoit de l'extérieur pour s'en approprier quelques "objets" sous une forme particulière ou transformée. Formée initialement d'objets de science, les mathématiques se trouvent tiraillées à l'envi, vers l'enseignement, la psychologie ou la politique, pour ne citer que quelques directions principales de déformations. Cisaillées dans leur essence, elles n'en sont que plus passionantes.

"J'apprends donc je suis". Certains agissent pour apprendre. Moi je fais partie de ceux qui doivent apprendre pour agir. C'est comme ça! Il y a les primaires et les secondaires. Je fais certainement partie de ces EAS: "Emotif-Actif-Secondaire", dont il semble qu'ils soient associés aux caractères des passionnés. Les amoureux de la combinatoire y trouveront certainement une esquisse de leur caractère personnel dans le lien précédent.

Je vois la vie comme un apprentissage continu qui  s'impose à moi et qui m'impose, en passant, une impérative réflexion constante sur cet apprentissage et donc sur la vie elle-même. C'en est tellement évident que c'est inextricable. C'est sans doute encore un coup foireux des fractales qui m'attendent avec leur tire-boulettes à chacune de mes réflexions, et qui me crient "mais ce n'est pas aussi simple que ça!". Ma philosophie personnelle est sans doute posée.

L'apprentissage est peut-être ce rituel sacrificiel anxieux devant le sujet barré lacanien, inaccessible à lui-même et sans cesse à la recherche de l'Autre toujours inatteignable. C'est aussi sans doute la quête, un peu comme celle de Scrat à la recherche perpétuelle de son gland,

du symbole au sens étymologique du terme, ou bien pythagoricien, permettant laborieusement de réassocier les morceaux brisés, ou d'aller chercher un  sens caché. Sans relâche. 

J'ai peut-être choisi, à dessein, mais inconsciemment, l'un de ces trois métiers que Freud a définis comme impossibles: "Eduquer, guérir, gouverner". C'est sans doute cette impossibilité ontologique qui assure l'infini des possibles dans laquelle je me sens à l'aise. Mon cadre psychologique est sans doute posé.

Le langage est trop étriqué. Il faut lui adjoindre le code, le codage pour raisonner juste, pour dépasser les paradoxes, les approximations douteuses et les sorites. Seule difficulté, le code, souvent caché ou secret, reste ésotérique. Il peine à devenir "exo", pour faire un jeu de mot bien à propos.

Pour moi, le caractère exotérique des mathématiques, c'est leur aspect culturel, ou transversal. Transversales. Cette caractéristique m'a été donnée pour justifier leur absence dans les thèmes des Bulletins Electroniques. Une présence cachée immanente qui pousse à la transcendance. Certains diront qu'elles sont ludiques, d'autres que c'est une formation de l'esprit, une école de la rigueur, etc, etc... A chacun son packaging! Elles seront de toutes façons toujours trop quelque chose pour les uns et pas assez pour les autres... La barre est sensible. Difficile de garder la voie du milieu.

Les maths sont donc très émotives, actives et secondaires... Elles sont sans aucun doute passionnées et passionantes!