Tendance inquiétante sur l'intérêt "mathématique"
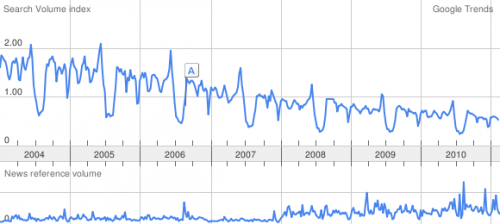
Google Trend permet de dresser des courbes associées aux requêtes sur certains mots-clés. Inutile d'être un expert pour voir que la tendance de recherche est décroissante sur le long terme pour "mathématiques" et "mathematics".
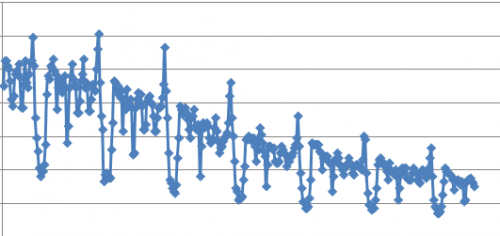
Le graphique précédent était en échelle relative, c'est à dire en fraction des recherches totales, mais le résultat n'est pas beaucoup plus réjouissant en échelle absolue sur la même période:
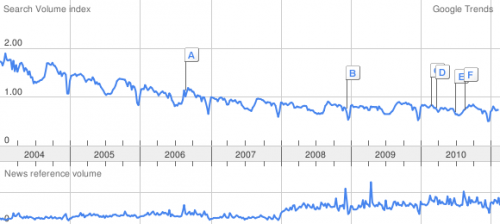
La tendance internationale suit la même pente...
Les origines des requêtes sont intéressantes à analyser, car elles ne sont pas sans surprise :
Pays:
| Pakistan |
| Philippines |
| India |
| Malaysia |
| South Africa |
| Singapore |
| Hong Kong |
| Australia |
| New Zealand |
Villes:
| Delhi, India |
| Chennai, India |
| Makati, Philippines |
| Kuala Lumpur, Malaysia |
| Mumbai, India |
| Singapore, Singapore |
| Hong Kong, Hong Kong |
| Sydney, Australia |
| Melbourne, Australia |
Langues:
| Tagalog |
| English |
| Chinese |
| Arabic |
| Dutch |
| German |
| Italian |
| Turkish |
| French |
La Chine n'est bien sûr pas présente dans ces statistiques puisque les requêtes se font majoritairement via Baïdu dans ce pays et non Google (le chinois est cependant la troisième langue mondiale utilisée, en dehors de la Chine!). Nous pouvons cependant remarquer que si la France est le pays des mathématiques, elle l'est peut-être en terme de médailles mais elle n'apparaît pas dans les dix premiers pays pour le nombre des requêtes et le français apparaît timidement en 9ème position pour les langues utilisées. Il est à noter l'allemand se porte plutôt bien, nous sommes derrière la Turquie et de façon assez surprenante, l'anglais n'est pas la première des langues apparaissant dans cette analyse mais le tagalog que je ne connaissais même pas de nom!
Les Etats-Unis sont aussi les grands absents de ces données!
A méditer.