L'extension du concept de partage numérique
Je suis pourtant un habitué des technologies numériques mais il est vrai que jusqu'à maintenant j'utilisais exclusivement un ordinateur. Aujourd'hui je possède un Smartphone et je viens de prendre conscience que l'idée que je me faisais du partage relevait de la préhistoire numérique, du temps du web 2 en quelque sorte où étaient (et sont encore) entassés sous chaque page ou billet, les icônes des principaux réseaux sociaux et sites de partage. On y voyait aussi une icône faisant figurer un mail, un pdf ou une imprimante. On pouvait aussi partager sur twitter ou sur Facebook. J'avais il y a quelques temps fait un billet sur le partage de fichiers en ligne, qui me paraissait déjà un élément très important pour un usage scolaire, c'est ici.
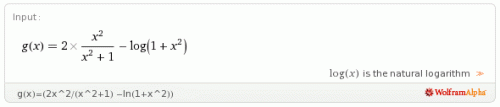
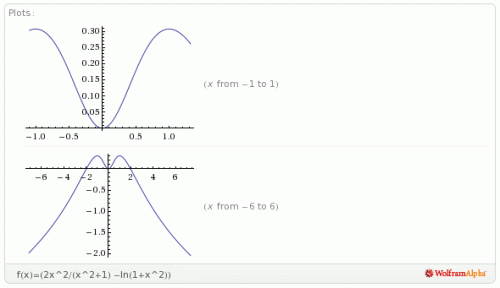
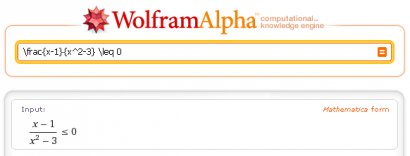
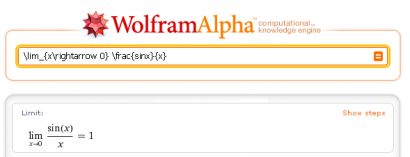
Je vais développer un peu plus en vidéo ce que j'entends par la notion de partage généralisé en partant d'un calcul effectué avec l'application Wolfram Alpha que j'ai téléchargée sur mon SmartPhone.
J'aurai pu prendre un autre exemple, une page web, une adresse physique ou une photo mais j'ai trouvé que le partage d'un résultat mathématique me semblait pertinent sur un blog de maths :
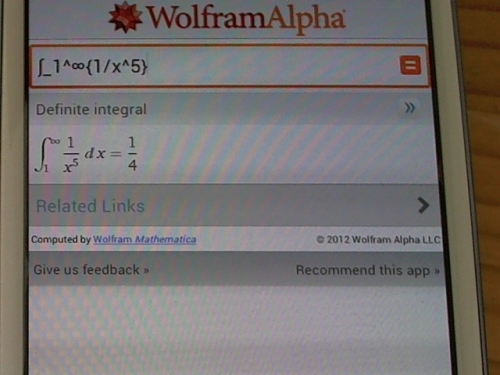
Ce qui est intéressant de considérer dans les vidéos qui vont suivre , c'est que le partage peut-être défini précisément (modification du texte dans le cas présent), il est dynamique (le contenu n'est pas figé, ici il s'agit d'un calcul que l'utilisateur pourra modifier) et qu'il peut se faire sur des supports ou applications de nature complètement complètement différentes (mail, réseaux sociaux, ordinateur, smartphone, signets personnels, QR code et même sur ce blog par l'intermédiare d'un envoi sur une adresse mail spécifique!). L'objet numérique sera suivant le cas, partagé de façon individuelle ou collective, publique ou privée, selon le mode de partage choisi).