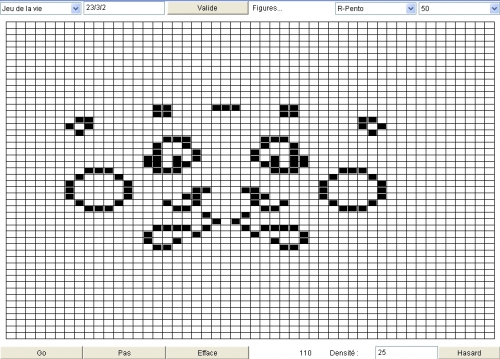
Le jeu de la vie est ce que l'on appelle un automate cellulaire. Il n'y a pas besoin d'être deux pour y "jouer". Il faut se munir d'un quadrillage sur lequel on place au hasard, ou pas, des jetons ( ce sont les cellules).
Les règles du "jeu" sont d'une simplicité incroyable mais les évolutions, d'une complexité terrible, à tel point que l'issue du jeu est indécidable, c'est à dire qu'il n'existe aucun procédé permettant de connaître pour toutes les configurations initiales comment va évoluer le jeu de la vie dans le futur.
Quelles sont ces règles ?
Si une case vide touche exactement trois jetons, alors on met un jeton sur cette case.
Si un jeton touche exactement deux ou exactement trois jetons, alors on le garde sinon on l'enlève.
Puis on regarde ce qui se passe au bout d'un grand nombre de tours de jeux, que l'on appelle itérations.
Les résultats sont surprenants !
Apparaissent des canons à planeur, un clown ou un jardin d'Eden qui, quant à lui, est une configuration impossible à atteindre, quelque soit la situation initialement choisie.
![727860947[1].gif](http://www.inclassablesmathematiques.fr/media/00/02/1615069423.2.gif)
Cliquer sur l'image pour voir différentes configurations de base évoluer.
Pour faire apparaître le clown c'est très simple, il suffit d'aller ICI, d'appuyer sur GO, de sélectionner le jeu de la vie (par défaut) à gauche et 50 à droite pour voir les cases, de cliquer sur 7 cases au milieu de l'échiquier en formant un U orienté vers le bas et de cliquer 110 fois sur "Pas" en bas. La tête de clown sera au rendez-vous.
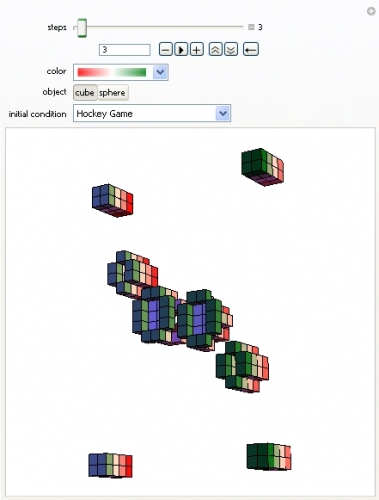
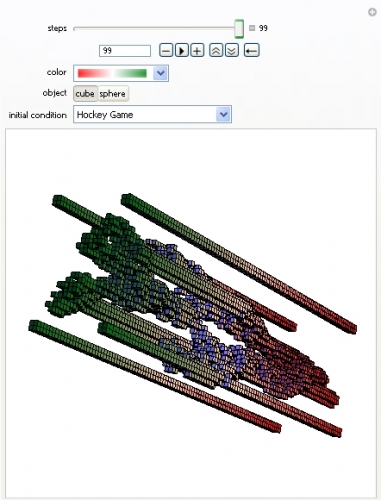
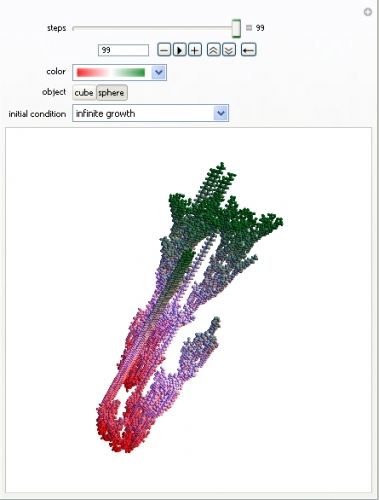
Wolfram a eu l'idée d'empiler les états du jeu les uns sur les autres, ce qui donne pour chaque configuration initiale, une structure tridimentionnelle. Il est ainsi plus facile de suivre l'évolution dans le temps de configurations initiales particulières.
Le rouge indique la configuration initiale et le vert l'état du jeu après le nombre d'itérations indiqué.
Et la question qui reste encore non-résolue est pourquoi cette configuration s'appelle Hockey Game ?
Pour visualiser les animations dynamiques de Wolfram, il faut télécharger le player gratuit.
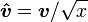 Alors que je consultais paisiblement mon Google Reader, je fus interpelé par un article intitulé "Fast inverse square root", partagé par un internaute du Monde. Je connaissais bien la traduction en français de tous les mots du titre: "Racine carrée inverse rapide". Chacun d'entre eux faisait sens mais lorsqu'ils étaient placés ensemble, je me retrouvais dans l'incapacité de prédire un contenu possible de l'article en question. J'imaginais bien sûr qu'il devait s'agir d'une méthode, exotique ,ça je ne le savais pas, mais certainement numérique pour calculer l'inverse d'une racine carrée de façon rapide.
Alors que je consultais paisiblement mon Google Reader, je fus interpelé par un article intitulé "Fast inverse square root", partagé par un internaute du Monde. Je connaissais bien la traduction en français de tous les mots du titre: "Racine carrée inverse rapide". Chacun d'entre eux faisait sens mais lorsqu'ils étaient placés ensemble, je me retrouvais dans l'incapacité de prédire un contenu possible de l'article en question. J'imaginais bien sûr qu'il devait s'agir d'une méthode, exotique ,ça je ne le savais pas, mais certainement numérique pour calculer l'inverse d'une racine carrée de façon rapide.




![727860947[1].gif](http://www.inclassablesmathematiques.fr/media/00/02/1615069423.2.gif)