L'univers numérique d'un prof de maths #9
Ça fait maintenant plus de deux ans que je n'avais pas publié un tel billet. C'était en août 2014. Vous pourrez ainsi remonter le temps jusqu'au premier billet de la série publié il y a maintenant 10 ans. Que le temps passe!
Alors quoi de neuf docteur? Attendez je relis le billet de 2014!
J'ai créé un site professionnel avec ScenariChain, que SFR a brutalement supprimé en fermant ses pages persos! J'héberge le site maintenant sous un nom de domaine personnel. Je l'utilise à partir d'un ordinateur connecté à Internet en classe et les élèves peuvent le consulter à domicile ou sur smartphone (même s'il n'est pas responsive design). Il contient des cours, des liens d'exerciseurs (Euler, Wims), des liens vidéos... Je n'emporte plus en classe mon ordinateur (Lenovo Yoga 2 passé sous Windows 10) .
J'ai créé un dossier partagé OneDrive et j'y partage des images réalisées en classe avec mon smartphone. Il s'agit de photos de tableau, de photos de cahiers d'élèves, de photos de corrigés. Je trouve des immenses avantages à cela: reprendre un exercice, utiliser une image en fond, laisser une trace pendant un certain temps, partager des cours et des corrections pour les absents.
J'utilise des quiz (exemple), non pas pour évaluer les élèves en cours ou en fin de notion, mais un peu comme "situation-problème" en début d'apprentissage. Les questions sont construites de façon à faire appel à des compétences et des connaissances antérieures (quand cela est possible). Je peux faire un peu de cours en amont ou durant le quiz. Chaque question minimise le nombre de concepts nouveaux, qui s'enchainent au fur et à mesure. Les variables didactiques peuvent être mieux appréhendées et circonscrites.. Le départ des notions nouvelles est une question et non une réponse. L'apprentissage est dynamisé et facilité. Les fiches de quiz sont réalisées avec les questions à gauche et un espace à droite laissé libre pour les justifications, les graphiques, les points de cours. Je demande aux élèves de distinguer leur réponse de la bonne réponse avec un code couleur et de compléter les encadrés de droite en vue de leurs révisions futures.
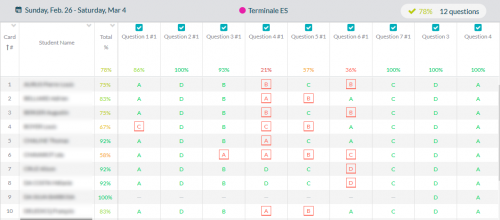
La scénarisation en classe se fait avec l'application Plickers, ce qui permet de distinguer très rapidement les points qui ne posent aucune difficulté, de ceux qui sont faiblement réussis et qui nécessitent donc une attention accrue. Les élèves sont plus engagés dès le début de l'apprentissage et confrontés à l'ensemble de la classe. Je récupère les évaluations sur le site, et je note les résultats sur une enveloppe individuelle qui contient le QR Code de chaque élève, distribué en début de séance. Je récupère la fiche entière complétée dans l'enveloppe et j'évalue le travail de structuration des connaissances, de justification, présent sur la partie droite de la feuille.
J'utilise toujours Edmodo (tutorat) et Diigo ( collection de liens étiquetés). J'ai abandonné tout le reste.
Pour résumer, j'utilise aujourd'hui pleinement le potentiel pédagogique ( et de simplification) procuré par la chaine numérique:
Smartphone+ Ordinateur connecté à Internet+ vidéo-projecteur.