Anaxagore
L'homme est intelligent parce qu'il a une main.

En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies. Ces derniers assurent le bon fonctionnement de nos services. En savoir plus.
L'homme est intelligent parce qu'il a une main.

Aussi curieux que cela puisse paraître, il est possible de creuser un "tunnel" dans un cube pour y faire passer un cube plus grand, certes plus grand de peu, mais néanmoins plus grand. En effet nous allons voir qu'il est possible de creuser un cube d'arête 29 pour y faire passer un cube d'arête 30.
Le dossier complet de Jean Lefort : ICI
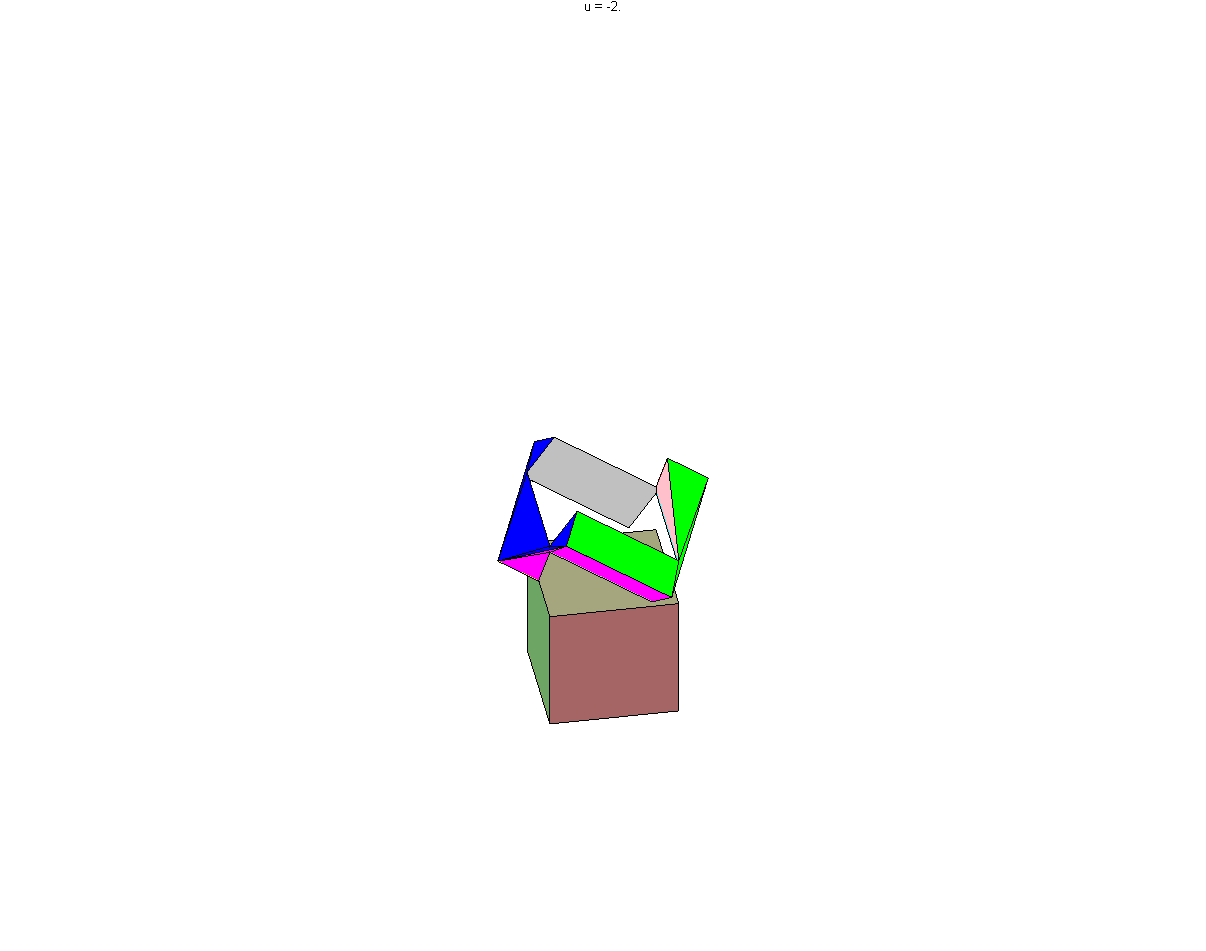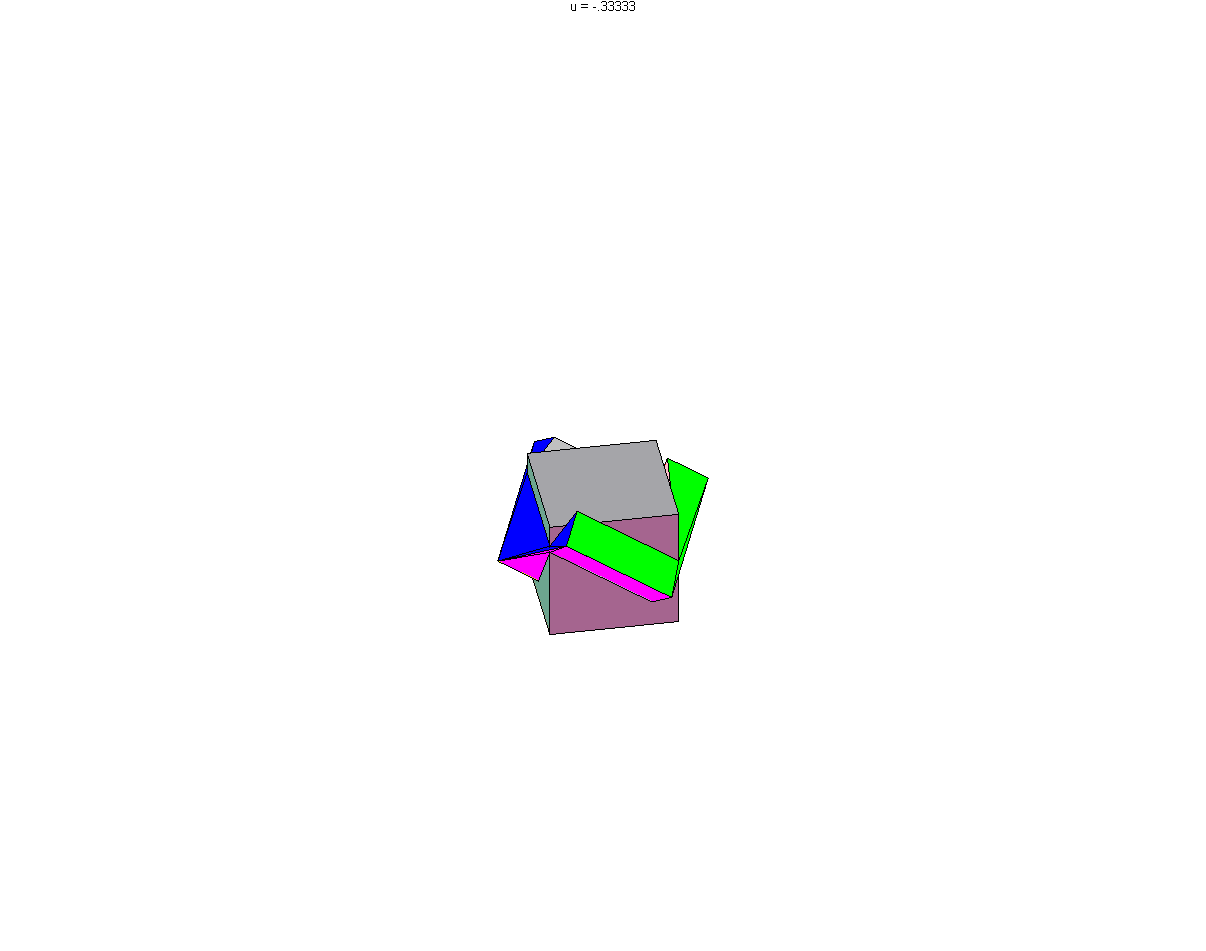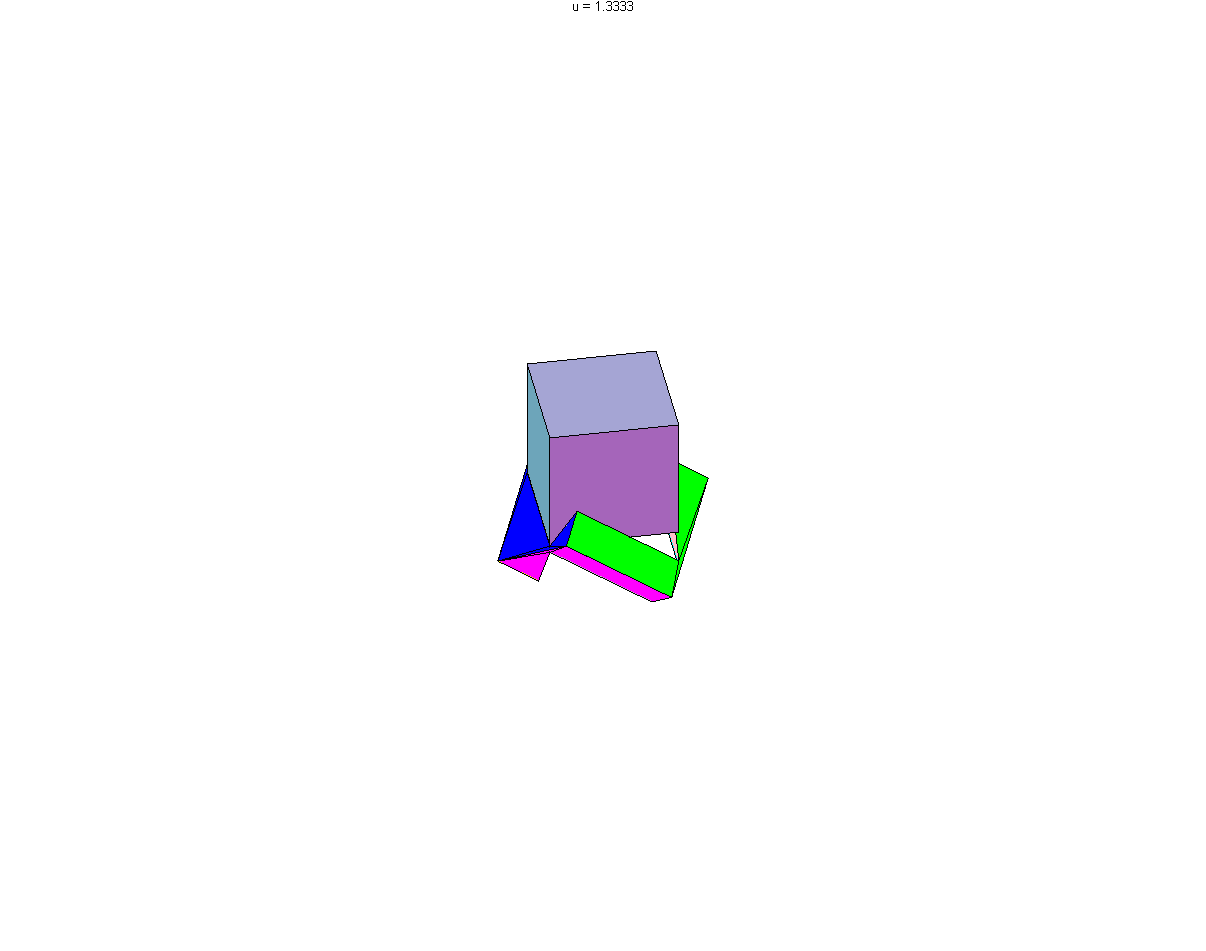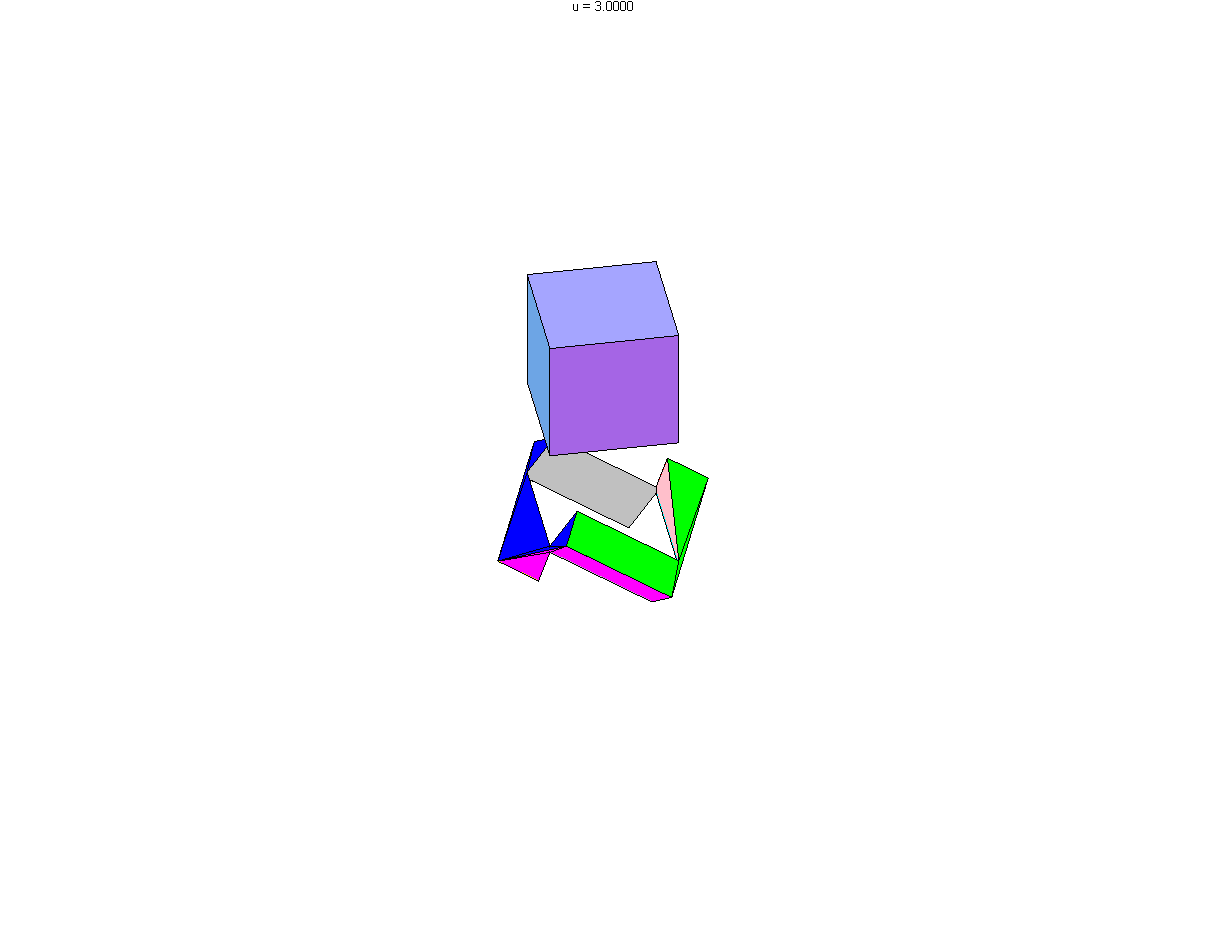
 La création de mondes virtuels visuellement acceptables est encore aujourd'hui réservée à des graphistes ayant des compétences en modélisation et dotés d'un certain sens artistique. Dans le cas particulier des univers ou jeux en ligne en 3D tels Second Life, un problème récurrent se pose : comment peupler ces espaces avec des objets dont le design est réaliste tout en étant simples à créer pour des non-spécialistes ?
La création de mondes virtuels visuellement acceptables est encore aujourd'hui réservée à des graphistes ayant des compétences en modélisation et dotés d'un certain sens artistique. Dans le cas particulier des univers ou jeux en ligne en 3D tels Second Life, un problème récurrent se pose : comment peupler ces espaces avec des objets dont le design est réaliste tout en étant simples à créer pour des non-spécialistes ?
Une équipe du laboratoire Virtual Worlds de l'université de Stanford a développé un logiciel qui répond en partie à cette question. Dryad est un outil en libre téléchargement qui permet à travers une interface graphique de créer très simplement des arbres réalistes en 3D, sans aucune connaissance en programmation. L'utilisateur peut interagir sur une série de paramètres qui caractérisent l'arbre : structure et inclinaison des branches, densité du feuillage, épaisseur et couleur du tronc, etc. Il a aussi la possibilité de naviguer parmi une forêt numérique générée dynamiquement, où les arbres proches présentent des similarités qui varient selon la direction empruntée. Une fois qu'un modèle satisfaisant est obtenu, celui-ci peut être exporté au format OBJ pour être ensuite modifié dans des logiciels de 3D plus classiques. Une copie est aussi envoyée à Stanford pour enrichir une base de données qui constitue un arboretum numérique.
Derrière ce processus de création simplissime se cache une série de propriétés mathématiques. Chaque arbre est représenté comme un point dans un espace vectoriel aux nombreuses dimensions. La méthode d'analyse en composantes principales permet à l'utilisateur d'interagir facilement avec ces paramètres. Le modèle des mélanges gaussiens est ensuite appliqué pour assurer que les arbres générés soient proches d'arbres au préalable "validés", et ainsi éviter d'obtenir des configurations impossibles dans la nature.
L'équipe de Stanford a commencé à se focaliser sur la génération d'arbres car leur classification et leurs caractéristiques sont connues et clairement identifiées. Mais Dryad doit avant tout être considéré comme une preuve de faisabilité, et compte bien appliquer le concept à la création de modèles représentant d'autres plantes, animaux, humains ou bâtiments. La génération assistée ou automatisée de mondes virtuels réalistes peut trouver une application directe dans les jeux vidéo, mais on peut également imaginer retrouver ces technologies dans les outils de navigation par satellite ou les logiciels de modélisation 3D.
Source Bulletins-électroniques : ICI
Quoi de "neuf" dans le "8" ? Rien de spécial mais Culturemath nous propose en guise de carte de voeux, un carnet original retraçant les principales dates anniversaires se terminant par 8 en rapport avec les maths et les mathématiciens !
Il y a 150 ans, était par exemple découvert le célèbre Ruban de Möbius !
Besoin d'un petit recyclage ?

 C'est le titre d'un article de l'hebdomadaire " Courrier International " n° 896 du 2 janvier 2008. Cet article s'appuie lui-même sur un sujet traité par "New Scientist". Le texte n'est malheureusement pas disponible en ligne. Je consacre donc cette note à sa synthèse.
C'est le titre d'un article de l'hebdomadaire " Courrier International " n° 896 du 2 janvier 2008. Cet article s'appuie lui-même sur un sujet traité par "New Scientist". Le texte n'est malheureusement pas disponible en ligne. Je consacre donc cette note à sa synthèse.
Évaluer le nombre de morts de la Seconde Guerre Mondiale : les historiens avancent le chiffre de 50 millions d'individus, mais les estimations varient suivant les méthodes utilisées et les sources entre 41 et 70 millions.
Consulter le registre des armées n'est pas suffisant pour comptabiliser ces pertes, il faut aussi inclure dans les conséquences des conflits, les décès causés par la malnutrition et les épidémies. Comment interpréter un logement vacant? Est-ce la mort des résidents ou leur exode qui en est la cause?
L'évaluation de l'impact d'un conflit ou la décision d'une aide humanitaire d'urgence se trouvent confrontées à ces obstacles. Une simple erreur d'estimation peut laisser des civils sans nourriture ou des crimes de guerre peuvent passer inaperçus.
En temps de paix, les informations sont collectées par le recensement. On peut même utiliser le confort du téléphone pour y accéder. Mais en temps de guerre, ce travail est beaucoup plus difficile et dangereux. Dans la pratique, la technique dite d'"échantillonnage par grappe" est utilisée. Celle-ci a été développée à l'origine pour évaluer l'impact des campagnes de vaccination. Les grappes sont des échantillons géographiquement déterminés représentatifs de la population et de sa densité. Des relevés au hasard sont effectués. Pour se faire, des équipes scientifiques doivent se déplacer sur les lieux, en étant la plupart du temps accompagnées par des gardes armés afin d'interroger les individus ou constater leur absence. Sans de sérieuses précautions ou lorsque la vigilance des enquêteurs s'affaiblit, ces chercheurs peuvent être confondus avec des agents du camp adverse et violentés. C'est d'ailleurs ce qui est arrivé, à deux membres d'une équipe norvégienne, en 1992 au Mali.
Chaque jour des scientifiques risquent leur vie dans les régions les plus violentes du monde pour exercer leur métier mal connu du grand public: déterminer le nombre de victimes d'un conflit de la façon la plus rigoureuse possible.
De la qualité de ces études dépend l'utilisation que l'on peut en faire. C'est par exemple l'une d'entre elles qui a servi à juger Slobodan Milosevic.
La difficulté de prélèvement des informations sur le terrain n'est pas la seule. Les autorités des pays concernés par les enquêtes peuvent voir d'un très mauvais oeil des statistiques qui ne leur conviennent pas, pouvant nuire à leur image ou à celle de leur pays. La publication des résultats se voit freinée ou même interdite, d'autant plus que ces états sont souvent partenaires et détiennent les cordons de la bourse.
Les ONG sont souvent les plus proches du terrain pour réaliser ces enquêtes, mais elles manquent de temps et de moyens pour les effectuer dans de bonnes conditions. En 2002, une analyse d'enquêtes a permis de suivre celles qui ont été réalisées par 9 ONG différentes sur 67 grappes d'individus. Il s'est avéré que seulement 6 d'entres elles étaient suffisamment rigoureuses. Ce manque de rigueur est d'ailleurs souvent avancé pour discréditer les enquêtes et leurs résultats lorsqu'ils ne sont pas conformes aux attentes.
Une étude sur la mortalité en Irak après l'invasion américaine de 2003 par des chercheurs du Maryland et des irakiens a été publiée dans The Lancet. Dans 47 grappes d'individus, on a sélectionné au sein de chacune, 40 familles qui ont été interrogées. Le résultat de l'enquête est effrayant, puisqu'avec cette méthode, le nombre de morts estimé serait de 655 000 au lieux des quelques dizaines de milliers couramment évoqués. G W Bush et Tony Blair ont écarté les résultats de cette enquête embarrassante. Certains opposants se sont même attaqués à la méthode elle-même. Parmi toutes les critiques évoquées, les spécialistes de la question ont émis les critiques les plus justifiées par rapport aux autres. Ils ont soulevé le problème du "biais de l'artère principale" qui pourrait être une source potentielle d'erreurs. Il se résume ainsi : dans chaque grappe urbaine, les ménages sont sélectionnés à partir d'une rue commerçante, puis dans une rue perpendiculaire résidentielle une maison est choisie au hasard afin de débuter l'enquête de terrain. Il pourrait y avoir ici, selon certains chercheurs, un impact sur les résultats de l'enquête en avançant comme argument que les rues coupant les artères principales sont privilégiées au dépend de rues plus éloignés faisant moins l'objet de combats. Cet argument est réfuté par les initiateurs de l'enquête qui affirment la pertinence de leur processus de sélection.
 Le débat reste ouvert en attendant de futures publications sur le sujet. Malgré cela les scientifiques continuent à exercer leur dangereux métier, dont la principale motivation est "de permettre à ceux qui se trouvent dans ces situations de se faire entendre".
Le débat reste ouvert en attendant de futures publications sur le sujet. Malgré cela les scientifiques continuent à exercer leur dangereux métier, dont la principale motivation est "de permettre à ceux qui se trouvent dans ces situations de se faire entendre".