Lancement d'un nouvel outil de débat sur Internet : "Opinion Space"
The Berkeley Center for New Media à l'University of California, Berkeley, a lancé un nouveau système de cartographie permettant de visualiser de façon claire et représentative un ensemble d'opinion sur des sujets d'actualité. Selon .C. Berkeley Professor Ken Goldberg, membre de l'équipe qui a développé ce projet "Les nouveaux outils ont besoin d'engager activement les groupes sur Internet sur des sujets allant de l'art à la politique publique". Ceci devrait encourager le dialogue et la confrontation des idées entre les utilisateurs d'Internet. Le nom du nouvel outil : "Opinion Space".
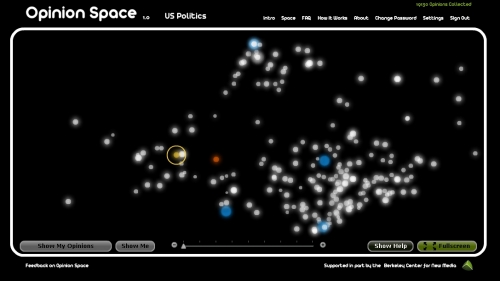
Le concept : chaque utilisateur est interrogé à propos de cinq affirmations et code son degré d'approbation ou désapprobation. En plus il peut ajouter un commentaire libre. Ainsi recueillies, les opinions de chacun apparaissent sous la forme d'étoiles dans une constellation. Plus des opinions sont similaires et plus leurs étoiles sont proches. Le système s'appuie sur les méthodes mathématiques appelées Analyse en Composantes Principales (ou PCA en anglais). Cette solution mathématique a été choisie car elle permet de représenter plus fidèlement l'ensemble de l'opinion d'une population qu'une méthode linéaire, comme l'explique Howard Rheingold auteur de Smart Mobs "les listes linéaires sont souvent dominées par des interventions extrêmes qui peuvent simplifier à l'excès et cacher une grande variété de points de vue". Les utilisateurs peuvent manipuler une échelle pour accréditer ou discréditer une déclaration. Sur une question qui change toutes les 2 semaines, ils peuvent également entrer leurs propres réponses écrites. Il est également possible de faire évoluer sa propre opinion et de changer le placement de l'étoile dans la constellation au fil du débat. Enfin chacun peut également lire les commentaires des autres et les évaluer. Selon Jay Walsh le directeur du service de la communication de Wikimedia "Une collaboration massive est conduite par les personnes passionnées, avec des points de vue différents provenant d'expériences différentes. "Opinion Space" est un nouvel outil de visualisation excitant qui aide les personnes à apprendre et à interagir entre eux. Cette prise de conscience mutuelle pourrait avoir des implications profondes".
La première constellation, et les premières questions d'"Opinion Space" portent sur la politique américaine. Plus largement, elles couvrent l'économie, l'éducation et l'environnement. Les chercheurs de Berkeley ont également prévus d'affiner le système en ajoutant de nouvelles fonctions et de nouvelles caractéristiques. D'autre part l'outil inclut des marques spéciales sous forme de points bleus qui représentent les opinions de personnes importantes qui ont été extrapolées en fonction des convictions qu'ils affichent. Par exemple dans cette première série de questions on peut trouver l'opinion de Rush Limbaugh, Arnold Schwarzenegger, Nancy Pelosi et Ralph Nader.
http://www.bulletins-electroniques.com/actualites/59079.htm