Le Graal des mathématiciens

Une hypothèse d’apparence anecdotique avancée par Bernhard Riemann il y a cent cinquante ans au sujet d’un problème classique, la répartition des nombres premiers, focalise l’intérêt des plus grands mathématiciens. David Hilbert en avait fait le huitième problème de sa célèbre liste. Au moins une dizaine de médailles Fields l’ont étudié… En 2005, il manque toujours le maillon qui permettra une démonstration plausible.

L'article du HS n° 20 de " La Recherche" - 2005 : ICI

« Jusqu’à ce jour, les mathématiciens ont en vain tenté de découvrir un ordre dans la suite des nombres premiers, et nous avons des raisons de croire que c’est un mystère que l’esprit ne pénétrera jamais. »

Leonhard Euler

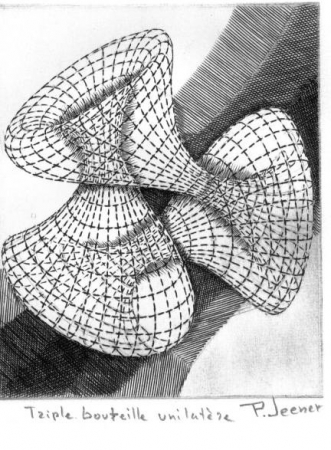
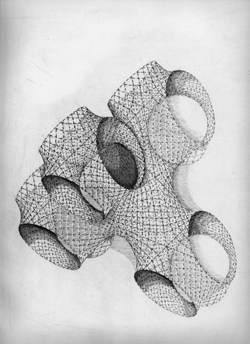
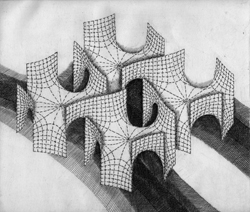
La première fois que j'ai vu Patrice Jeener, j'ai cru que c'était Merlin l'enchanteur avec une longe toge, ou peut-être Socrate, enfin un personnage atemporel, en dehors de tout temps et en particulier de celui qui s'écoule lorsqu'il réalise des gravures de formes mathématiques. Car pour faire de la gravure, il ne suffit pas de savoir dessiner, il faut prendre une plaque de cuivre...et son temps pour la graver. Les résultats sont surprenants et eux-aussi atemporels. Les gravures de Patrice mêlent la tradition de la gravure à la plus grande modernité, la matérialité du burin à l'immatérialité du calcul numérique. Les formes sont sans limites ainsi que l'imagination de l'artiste qui transforme, sur ces gravures récentes, quelques surfaces et volumes de l'espace en une allégorie joyeuse de la création divine.

Je vous présente ici quelques gravures, dont la première, le S.M. orthorhombique m'a été envoyée par Patrice spécialement pour la publication sur ce blog.

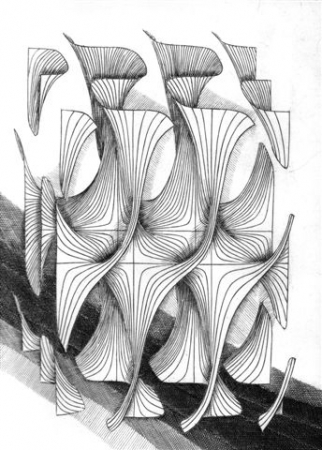
On pourra découvrir la triple bouteille de Jeener-Klein, transcrite par J.F. Colonna :

Quelques gravures de surfaces minimales et extensions de Jeener ainsi que les transcriptions de J.F. Colonna: ICI

On trouvera aussi dans cette revue des oeuvres de Patrice Jeener : ICI

Les dossiers de l'ingénierie éducative
scérEn

Un état des lieux de l’univers TICE et mathématiques.
Comment le tableur, la calculatrice ou le logiciel de construction géométrique apportent une aide sensible dans l’élaboration d’une démonstration, la conjecture d’un résultat, la modélisation d’une situation ou la représentation d’un concept…
Des scénarios racontés avec assez de précision pour faire voir comment s’imbriquent l’outil et son exploitation pédagogique.
Les points de vue de l’Inspection générale, de la direction de la Technologie, de l’association Sésamath, et ceux de chercheurs, d’enseignants, de créateurs de sites.

La revue téléchargeable en format PDF : ICI

Lire par exemple

Des outils numériques pour l’enseignement des mathématiques de Jacques Moisan ICI

Rétrospective, pistes d’usage et essai de prospective, l’usage des TICE dans l'enseignement des mathématiques de Didier Missenard : ICI

La base Educnet : ICI

Toute la collection de ces dossiers : ICI

Dans l'histoire des nombres, il est quelquefois difficile de faire la différence entre un zéro linguistique, indiquant une absence ou un vide, ou un zéro ayant statut de nombre. En 458, un texte en sanscrit traitant de cosmologie, le Lokavibhaga, est la plus ancienne attestation connue de l'emploi du zéro, qu'on écrit "vide" (en sanscrit !) pour indiquer une unité manquante. Le premier zéro sous la forme d'un rond semble être apparu en 605 dans ce qui est actuellement le Cambodge... mais si cette région était sous tutelle chinoise à l'époque, elle pratiquait de nombreux échanges avec l'lnde: chacun y retrouvera ses petits ! Dans "Le calcul indien'' cité plus haut, Khwarizmi écrit à peu près: ''pour que la position ne soit pas vide, on écrit un petit cercle en forme de O n'ayant aucune signification". Vers 850, Mahavira définit enfin le zéro comme Ia somme de deux nombres opposés. On connaît la suite.

Le fichier PDF de Michel Soutif qui précise les connaissances sur l'apparition du zéro dans " La numération décimale de position " ICI

La page dont est extraite le texte ci-dessus : ICI

L'histoire ( rapide ) des zéros : ICI et ICI

La notion de vitesse fait maintenant partie de notre vocabulaire courant: les radars contrôlent celles des véhicules, aller vite pour faire nos courses, imaginer une vitesse de décompositition est commun: l'idée même de vitesse telle qu'on l'entend aujourd'hui n'a pas toujours été unifiée ni  quantitative, elle faisait plutôt partie des concepts qualitatifs comme la luminosité, la couleur. L'émergence du "nombre vitesse" n'a pas été précurseur lorsque qu'on lui affectait des attributs de " plus " ou "moins" - de magis et minus - comme pour le blanc par exemple lorsque l'on précise plus ou moins blanc. La notion moyenageuse de vitesse correpondrait plus à notre notion de rapidité.  

C'est Nicole Oresme qui a été le principal artisan médiéval du travail  sur la notion de vitesse, il a énoncé la règle Merton utilisée du XIVème siècle jusqu'au XVIème siècle. Elle  affirme l'équivalence du mouvement uniformément  varié et  du mouvement dont le degré moyen de vitesse est la moitié du mouvement donné. Pour cela il suffit de faire un graphique où le temps est en abscisses et la vitesse en ordonnées. On remarque que l'aire du triangle ou du rectangle suivant le type de mouvement sont égales et correspondent à la distance parcourue. Ce n'est pas pour autant que la notion de "vitesse quantitative" se dégage clairement!

Pour passer " à la vitesse supérieure" sur la notion de vitesse, il faudra attendre Cavalieri, Fermat et ICI et Pascal.

L'article passionnant La Mécanique. Une Science médiévale ?  ICI .