De l'interprétation des résultats du PISA en mathématiques
 On peut s'interroger à juste titre sur la lecture des résultats de l'enquête PISA qui place la France en 18ème position et au 17ème rang pour les mathématiques. La politisation de leur interprétation est un phénomène croissant qui mérite aussi d'être souligné. L'école a-t-elle besoin de ce débat? J'ai publié, il y a plus d'une semaine ( le 30/11), un article intitulé "
On peut s'interroger à juste titre sur la lecture des résultats de l'enquête PISA qui place la France en 18ème position et au 17ème rang pour les mathématiques. La politisation de leur interprétation est un phénomène croissant qui mérite aussi d'être souligné. L'école a-t-elle besoin de ce débat? J'ai publié, il y a plus d'une semaine ( le 30/11), un article intitulé "
Les écoliers français médiocres ". J'ai cette naïveté de croire que les personnes lisant de tels articles vont forcément s'interroger sur les conditions de l'enquête, sur les buts recherchés et donc prendre avec la plus grande précaution, les résultats bruts afin de les interpréter. Lorsque je relais un article, ce n'est pas qu'il reflète une position personnelle mais que j'ai jugé le sujet suffisamment intéressant pour faire débat ou servir de matériau pour une réflexion un peu plus poussée, ce que je n'ai pas toujours le temps de faire. Au sujet de ce classement, les commentaires vont bon train et sur les blogues, on trouve des titres tels que: La France fabrique-t-elle des crétins ? Baisse du niveau scolaire en France, Education Nationale et Nullitude, Un niveau scolaire moyen pour une puissance moyenne.
On peut lire un peu partout, la brève analyse et la solution "miracle" d'Eric Charbonnier : “La France doit diminuer sa proportion d’élèves en difficultés (20%) et augmenter sa proportion d’excellents élèves pour pouvoir s’améliorer dans les classements internationaux”, ses préconisations sont simples : “peut-être d’alléger les programmes scolaires et de mettre en place des heures de soutien pour les élèves les plus en difficulté”.
Tout cela se mort un peu la queue. Alléger les programmes pour que le niveau monte! Déjà que certains se plaignent qu'on n'apprend plus rien à l'école et comme recette pour augmenter le proportion d'excellents élèves, c'est plutôt surprenant. Bonne ou mauvaise idée? Si quelqu'un détenait la recette " globale et totale", à un problème aussi complexe, ça devrait se savoir... chaque stratégie éducative a des avantages et des inconvénients qu'il faut assumer. Loin de tels débats, l'enquête PISA réduit les performances globales d'un système éducatif à un seul chiffre: sa position par rapport aux autres pays.
Mais quel est le rapport entre la Finlande, la France, Je Japon et la Corée pour que l'on puisse ainsi mettre en rapport leurs stratégies éducatives qui répondent souvent à une problématique historique qui leur est propre?
Le problème de l'intégration se pose-t-il au Japon et en Finlande? Qu'en est-il du nombre d'habitants de tel ou tel pays, de la centralisation ou de la décentralisation des systèmes. La France est l'un des pays qui fait le plus redoubler, ceci à cause du contenu très ambitieux de ses programmes ( il suffit par exemple d'avoir enseigné le programme de mathématiques en 4ème pour le savoir ), c'est un choix, qui mérite peut-être d'être revu, mais pour l'instant c'est le nôtre. Or l'enquête PISA s'appuie sur une tranche d'âge, ainsi donc les écoliers français n'ont pas la même maturité scolaire, ce qui fait que le critère " de même âge " n'est pas tellement adapté à notre système scolaire. L'enquête PISA , malgré des résultats positifs peut aboutir au paradoxe soulevé par Pierre Duhamel au Canada ICI:"Bref, trop de jeunes quittent trop tôt l’école. Mais ceux qui y restent obtiennent des résultats meilleurs que ceux de la plupart des élèves des autres pays. " Le Japon est quant à lui, tout simplement catastrophé : ICI et chaque pays va de l'autofélicitation à l'autoflagellation, suivant ainsi la diversité des attitudes possibles devant une bonne ou une mauvaise note. Certains ont même triché ( mais chut !)
Parmi tous les billets que j'ai lu, seul Guy Marion se penche réellement sur l'interprétation des résultats de l'enquête, en précisant:
Que valent les études PISA ?
Ces évaluations se fondent sur des tests que doivent passer un échantillon représentatif d'adolescents de 15ans (il s'agit d'une étude par tranche d'âge et non par niveaux scolaires), les états ayant la possibilité d'exclure une très faible proportion d'élèves en grande difficulté. Il est à noter que certains ont carrément triché en excluant un grand nombre d'élèves en difficultés (cas de la Corée du Sud qui a ainsi obtenu d'excellents résultats en 2003 !).
Les questions de ces tests sont majoritairement élaborées par un consortium de centres de recherche dirigés par un centre australien et dont les autres membres sont issus des pays suivants : États-Unis, Japon et Pays- Bas. La transparence n'est pas de mise : ce consortium garde secret l'immense majorité de ses questions, ne révélant que celles qui ont été rejetées ou ne sont plus utilisées.
La majorité de ces questions reflète l'origine en grande partie anglo-saxonne du consortium : beaucoup de QCM, questions s'inspirant plutôt de la vie quotidienne que d'exercices disciplinaires, styles de questions avec lesquelles les élèves français (et de nombreux pays latins) ne sont pas familiarisés. En outre, il s'agit plus dévaluer la façon dont les jeunes sont capables d'exploiter leurs connaissances dans leur pratique quotidienne
(conception plutôt anglo-saxonne de l'École) que leur niveau théorique dans tel ou tel domaine des Sciences ou des Lettres (conception plutôt en vigueur en France et dans les pays latins).
Des influences idéologiques sont perceptibles. Le commanditaire de ces études, l'OCDE est une organisation à but économique et non éducative.
On peut s'interroger sur la capacité de nos élèves à répondre à certaines questions qui peuvent leur sembler déroutantes ( ICI ) et le fait de convertir ensuite de tels résultats en "niveau de mathématiques" alors qu'aucune question faisant intervenir les théorèmes de Thalès et de Pythagore n'est par exemple posée, or c'est ce qui constitue pour la France, le coeur de l'enseignement de géométrie euclidienne jusqu'en seconde ( presque la moitié du temps ), rien non plus sur les puissances de 10, la mise en équations, problèmes difficles rencontrés par les élèves français tout au cours de leur scolarité...!
Il s'agit en mathématiques d'évaluer la culture mathématique et non les mathématiques elles-mêmes comme l'indique ce document PDF à partir de la page 81 ( à consulter impérativement ).
On y lira : La culture mathématique est l’aptitude d’un individu à identifier et à comprendre le rôle joué par les mathématiques dans le monde, à porter des jugements fondés à leur propos et à s’engager dans des activités mathématiques, en fonction des exigences de sa vie en tant que citoyen constructif, impliqué et réfléchi.
En France, les mathématiques ne sont pas du tout enseignées sous cet angle là. Est-ce bien ou mal? Ce n'est pas à moi d'y répondre, mais il me semble fondamental d'inclure cela dans l'interprétation des résultats de l'enquête que l'on fera.
Les exemples donnés dans ce dossier parlent d'eux-mêmes :
Exemple n° 1 : BATTEMENTS DE COEUR
Exemple n° 2 : VACANCES
Exemple n° 3 : COMPTE D’ÉPARGNE
Exemple n° 4 : PIÈCES DE MONNAIE avec ce petit bijou de justification introductive :
L’exemple n° 4 présente un problème où le contexte, imaginaire, est extra-mathématique.
D'autant plus que la première question de ce problème n'est pas très " académique", et si elle est tout à fait digne d'intérêt, elle n'en reste pas moins surprenante pour des élèves français:
Serait-il concevable de mettre en place un système de pièces de monnaie en n’utilisant que les valeurs 3 et 5 ? Plus spécifiquement, quels sont les montants qui pourraient être obtenus sur cette base ? Un tel système serait-il souhaitable ?
Exemple n°5 : EXCURSION SCOLAIRE
Exemple n°6 : PROLIFÉRATION CELLULAIRE
Exemple n°7 : PROIE-PRÉDATEUR
Exemple n°8 : GAUSS
Exemple n°9 : POURCENTAGES
Exemple n°10 : ÂGE MOYEN
Avec la belle question : Si 40 % des habitants d’un pays ont au moins 60 ans, est-il possible que l’âge moyen de la population soit de 30 ans ?
Exemple n°11 : AUGMENTATION DES REVENUS ?
Exemple n°12 : ACCROISSEMENT DE LA CRIMINALITE

Question 2 : ACCROISEMENT DE LA CRIMINALITÉ
Comment les graphistes s’y sont-ils pris pour établir ce graphique ? Et pourquoi ?
On lit : Les fabricants de systèmes d’alarme ont utilisé les mêmes données pour établir le graphique suivant ( non reproduit ici )
Or le graphique des vendeurs d'alarmes n'est pas superposable à celui du graphiste, ont lit pourtant que les données sont les mêmes ( en leur possession certes mais pas utilisées comme le dit l'énoncé!).... S'il semble évident que les poseurs d'alarme ont omis de reporter une partie des données pour faire leur graphique, la réponse à ces deux questions ne me semble pas du tout évidente pour un élève français de 15 ans qui n'est pas habitué au débat sur la "culture mathématique PISA" en mathématiques
ETC,ETC...
On peut donc s'interroger sur la capacité qu'ont les élèves français à répondre à ce type de questions lorsqu'on les entraîne depuis quelques années sur Thalès, Pythagore, les médianes, les médiatrices, les translations, les factorisations ou les identités remarqubles.
Ce qui est placé au centre de cette enquête n'est pas au sens strict, ce que l'on nomme en France " Mathématiques", ce qui ne retire en rien à la qualité de ces exercices, mais je le rappelle, doit être mis en avant, lorsque l'on se permet d'interpréter les statistiques brutes et devenir ainsi des sortes de vautours rassemblés autour d'une charogne que serait l'Education Nationale française, qui si elle ne réussit pas sur tous les fronts, n'échoue pas non plus sur tous.
Pour conclure, il ne me semble pas que l'enquête PISA soit la mieux placée pour évaluer le niveau de l'enseignement des mathématiques en France qui est, malgré cela, au premier rang mondial de la recherche mathématique : ICI
On peut d'ailleurs noter ce que PISA considère comme composantes de la culture mathématique :
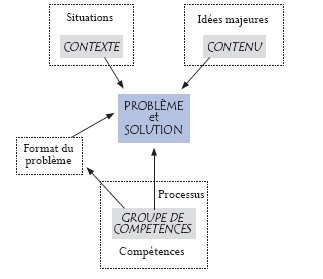
Si ces composantes sont très louables, ce n'est pas du tout l'angle sous lequel sont abordés les programmes de collège et de lycée où l'enseignement est plutôt basé sur la rigueur de la démonstration, la précision des justifications et sur une bonne pratique de la technique mathématique. On peut aussi se demander s'il n'y a pas de confusion entre les mathématiques et le discours autour des mathématiques, ce que résumerait la notion de "culture mathématique".
Je pense donc que c'est plus par la faible exposition de nos élèves à ce type de questions que par la faiblesse du système que nos élèves qui ne parviennent peut-être pas à y répondre en grand nombre. On peut voir aussi que de nombreuses questions traitent de %, et là encore ces questions sont traitées tardivement en BEP par exemple et si l'on sait que beaucoup d'élèves de BEP ont redoublé, il n'est pas évident qu'ils aient vus beaucoup de % à 15 ans puisqu'ils arrivent dans cette section vers 16 ans ! Pour les élèves d'enseignement général, je dirai qu'il en est de même puisqu'un chapitre est consacré sur ce sujet, seulement en première ES et que les élèves le trouvent très faciles !
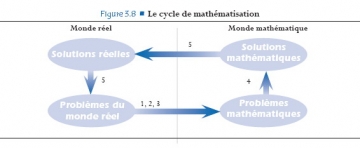
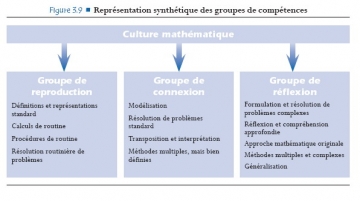
La synthèse finale de PISA : L’objectif de l’enquête PISA est de développer des indicateurs montrant dans quelle mesure les pays ont réussi à préparer leurs jeunes de 15 ans à devenir des citoyens actifs, réfléchis et intelligents, sous l’angle de leurs compétences en mathématiques. Dans ce but, PISA a élaboré des évaluations qui cherchent à définir dans quelle mesure les élèves sont capables d’utiliser ce qu’ils ont appris. Celles-ci mettent en avant l’utilisation des connaissances et des raisonnements mathématiques pour résoudre des problèmes issus de la vie de tous les jours et proposent une variété de problèmes mathématiques dans lesquels l’élève est confronté à des tâches plus ou moins guidées et structurées mais qui leplacent face à des problèmes authentiques, où il doit recourir à son propre raisonnement. Ce cadre d’évaluation décrit et illustre par des exemples la définition de culture mathématique adoptée dans PISA 2006 et pose le contexte des items. Les composantes principales du cadre d’évaluation des mathématiques (contextes d’utilisation des mathématiques, contenus mathématiques et processus mathématiques) sont cohérentes par rapport à celles des autres cadres d’évaluation PISA et découlent directement de la définition de la culture mathématique. La description des contenus et des contextes met l’accent sur les caractéristiques des problèmes auxquels les élèves sont confrontés en tant que citoyens, tandis que la description des processus met plutôt l’accent sur les compétencesutilisées par les élèves pour résoudre ces problèmes. Ces compétences ont été réparties en trois groupes de compétences pour faciliter le traitement de ces processus cognitifs complexes dans le cadre d’un programme d’évaluation structuré.
Pour revenir à la question de l'évaluation faite par PISA, je reste convaincu que ce n'est pas avec ce type de questions sur nos élèves de 15 ans que l'on peut corréler sans réserve, les résultats avec le niveau des élèves français. Pour ma part, en mathématiques, elle montre tout au plus un décalage entre ce qui est évalué, ce qui est enseigné et la façon dont ça l'est!
Il y aura cohérence entre les deux, lorsque les mathématiques concrètes seront devenues le centre de nos programmes et que la géométrie plane aura perdue sa place. Est-ce le seul type de changement possible pour notre enseignement ? On se pose visiblement en France la question de l'introduction forte des logiciels de géométrie dynamique dans l'enseignement secondaire finalisée par une épreuve pratique au bac. La fin de la géométrie plane ne semble donc pas sonnée, bien au contraire ( à moins que ne se produise un curieux effet de substitution de la démonstration manuelle par la vérification logicielle, pourquoi pas ).
Pour clore le sujet de l'interprétation des résultats, je me demande si, sous ces conditions, la variation des résultats de l'enquête peut être analysée comme une variation du niveau des élèves et non comme le témoin de l'incapacité de cette enquête à évaluer ce qui est enseigné réellement dans chaque pays. Si c'était effectivement le cas, cela rendrait la comparaison bien difficile compte tenu de la diversité des choix d'enseignement des différents pays concernés.
La question de la récupération politique des résultats de l'enquête prend ainsi tout son sens, et on pourra lire l'article suivant:
L'OCDE et partenaires sont de plus en plus préoccupés par la politisation des résultats du Programme International pour le Suivi des Acquis des élèves (PISA).
Avec l'annonce des derniers résultats de PISA 2006, les éducateurs ont été témoins de la même histoire se déroulant à travers le monde. Dans des pays où les étudiants sont arrivés près du sommet, les politiques se félicitent et prennent crédit pour une bonne politique de l'éducation. Dans des pays avec une réussite moindre, les politiques blâment le système scolaire et les enseignants pour une performance pauvre. Dans les deux cas, les rapports des médias tendent à se focaliser sur le classement et offrent une approche simpliste de style "tableau de ligue". La suite ICI
---------------------------------------------------
La réaction de Jean-Pierre Bouguignon ( PDF 1 page ): ICI
J'aime vraiment le slogan "Vous trouvez que l'éducation coûte cher. Essayez l'ignorance."
L'avant-dernière livraison de l'étude PISA avait montré que, si l'on "oublie" (ce qu'on n'a évidemment pas le droit de faire) les élèves qui ont vraiment décroché, les performances des élèves scolarisés en France, en mathématiques notamment, étaient au contraire assez remarquables. Il est donc important d'examiner si, dans cette livraison de l'évaluation, cette situation a évolué ou non.
----------------------------------------------------
Premières analyses DEPP : ICI
----------------------------------------------------
PISA : des indicateurs pour lutter contre les inégalités scolaires : ICI
 L’Académie des Sciences publie des Recommandations sur la formation des professeurs à l’enseignement des sciences, à l’occasion de l’intégration en 2007 des Instituts universitaires de formation des maîtres (IUFM) dans l’université et des réflexions nationales actuelles sur la condition enseignante.
L’Académie des Sciences publie des Recommandations sur la formation des professeurs à l’enseignement des sciences, à l’occasion de l’intégration en 2007 des Instituts universitaires de formation des maîtres (IUFM) dans l’université et des réflexions nationales actuelles sur la condition enseignante.