Graph le gentil grapheur
Graph est un grapheur très simple disponible en langue française. Il possède les fonctionalités élémentaires pour le rendre très efficace comme outil de visualisation en classe ou l'édition d'images à insérer dans un document mathématique. Il possède de plus une version limité esans la dérivation pour le collège ou la seconde.
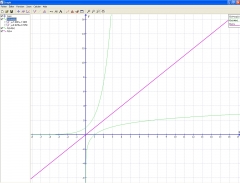
On entre les fonctions avec leur domaine de visualisation et leurs caractéristiques de représentation. Leurs expressions apparaissent à gauche de l'écran avec une case à cocher qui permet de sélectionner celles que l'on veut visualiser. Cette particularité est très pratique. Le seul inconvénient est que toutes les fonctions s'appellent f... ou alors je n'ai pas trouvé le moyen de les renommer!
Cliquez sur les images pour les agrandir
Dans la colonne de gauche en cliquant droit sur la fonction sélectionnée, apparaît un menu contextuel avec la possibilité d'éditer la fonction mais aussi d'insérer une normale ou un tangente, d'afficher la fonction dérivée ou d'afficher un remplissage.



 Le cancer est l'une des causes majeures de décès dans le monde (en particulier dans les pays en développement), avec environ 11 millions de personnes diagnostiquées et environ 7 millions de personnes qui meurent chaque année. Les prévisons de l'Organisation mondiale de la santé sont d'environ 9 millions de morts en 2015 et de 11,5 millions de décès en 2030 par cancer.
Le cancer est l'une des causes majeures de décès dans le monde (en particulier dans les pays en développement), avec environ 11 millions de personnes diagnostiquées et environ 7 millions de personnes qui meurent chaque année. Les prévisons de l'Organisation mondiale de la santé sont d'environ 9 millions de morts en 2015 et de 11,5 millions de décès en 2030 par cancer.