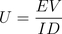Ne remettons pas à demain ce qui peut être dit aujourd'hui.
Le professeur Piers Steel, psychologue de l'université de Calgary, a passé plus de dix ans à comprendre pourquoi les personnes remettaient au lendemain ce qu'elles pouvaient faire le jour même.
Les procrastinateurs chroniques représentent 20% de la population. Ils sont plus impulsifs, irréguliers, moins soucieux des détails et de leurs obligations envers les autres.
L'équation qui régit la procrastination est la suivante :
U signifie l'utilité ou le désir d'achever une tâche donnée
E représente l'attente, l'espérance de son succès
V mesure la valeur de la réalisation achevée
I représente la rapidité d'éxécution de cette tâche
D mesure la sensibilité personnelle de la repousser à plus tard.
(j'ai essayé de traduire au mieux!)
Les psychologues avaient pour usage d'associer la procrastination aux seuls perfectionnistes qui évitent une tâche en raison de leur incapacité à atteindre un résultat parfait.
Ils devront maintenant faire un peu de mathématiques pour affiner leur diagnostic à moins qu'ils ne remettent à plus tard leurs conclusions!
Si vous avez des idées de travaux pratiques ou d'exercices...