 Un nombre 321 dit de Thābit pour Thābit ibn Qurra, est un nombre de la forme Kn=3·2n−1 , où n est un entier naturel.
Un nombre 321 dit de Thābit pour Thābit ibn Qurra, est un nombre de la forme Kn=3·2n−1 , où n est un entier naturel.
Pour les premières valeurs de n =0, 1, 2... ces nombres valent 2, 3, 5, 11, 23, 47, 95, 191, 383, 767, 1535, 3071, 6143, 12287, 24575, 49151, 98303, 196607, 393215, 786431, 1572863, 3145727... (Suite A055010).
Les premiers nombres de Thābit premiers appelés aussi 321-premiers sont : 2, 5, 11, 23, 47, 191, 383, 6143, 786431, 51539607551, 824633720831,... (Suite A007505).
La premières valeurs de n pour lesquelles on trouve des 321-premiers sont: 1, 2, 3, 4, 6, 7, 11, 18, 34, 38, 43, 55, 64, 76, 94, 103, 143, 206, 216, 306, 324, 391, 458, 470, 827, 1274, 3276, 4204, 5134, 7559, 12676, 14898, 18123, 18819, 25690, 26459, 41628, 51387, 71783, 80330, 85687, 88171, 97063, 123630, 155930, 164987, 234760, 414840, 584995, 702038, 727699, 992700, 1201046, 1232255, 2312734, 3136255, 4235414 (Suite 002235).
Les nombres premiers pour n≥234760 furent trouvés à partir de 2003 à l'aide du 321 project. Le plus grand d'entre eux a été découvert par Dylan Bennet en 2008 avec la valeur de n=4235414. Ce nombre possède 1274988 chiffres en base 10.
La représentation binaire de ces nombres est particulière. Elle est formée de 10 puis de n 1.
Par exemple pour K7=3·27−1=383, l'écriture binaire est 101111111.
Thābit ibn Qurra était un mathématicien, physicien, astronome et musicologue persan qui vécu de 826 à 901.
Il montra que si Kn, Kn−1, and 3×K2n−1 + 2 sont tous premiers, alors les nombres 2n×Kn×Kn−1, 2n×(3×K2n−1 +2) sont amicaux. Cette hypothèse se rencontre seulement trois fois, pour n = 2, 4, et 7, donnant les paires de nombres amicaux suivantes: (220, 284), (17296, 18416), et (9363584, 9437056). (Source: MathWorld et Wikipédia).
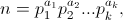



 Un nombre 321 dit de Thābit pour Thābit ibn Qurra, est un nombre de la forme Kn=3·2n−1 , où n est un entier naturel.
Un nombre 321 dit de Thābit pour Thābit ibn Qurra, est un nombre de la forme Kn=3·2n−1 , où n est un entier naturel. 
 Le 25 Juillet 2009 à 1 heure 11 minutes et 48 secondes UTC, le projet de recherche de
Le 25 Juillet 2009 à 1 heure 11 minutes et 48 secondes UTC, le projet de recherche de