Voici une collection d'extraits de films où apparaissent les mathématiques - des liens en bas de page : ICI

Je vous conseille la recette du cocktail de " Marius ".

Adresse trouvée  ICI

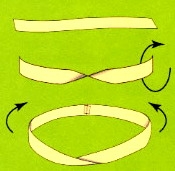Le ruban de Möbius est une surface à 2 dimensions possédant l'étrange propriété de n'avoir qu'une surface. Malgré cela, il n'en reste pas moins très facile à réaliser : il suffit de prendre une bande de papier suffisamment longue, de faire faire  un demi-tour à l'une de ses extrémités puis de rapprocher et coller les deux bouts de cette bande l'un à l'autre.
On peut se poser à juste titre la question de la forme que l'on obtient après avoir réalisé cette manipulation. Or jusqu'à maintenant aucune réponse précise n'avait été formulée à ce sujet.

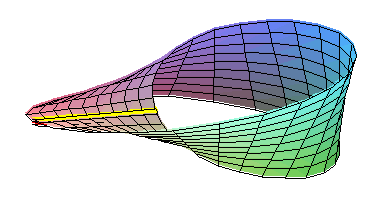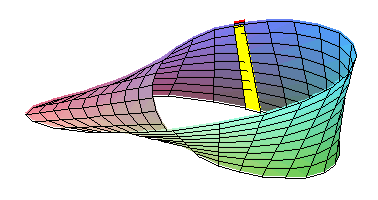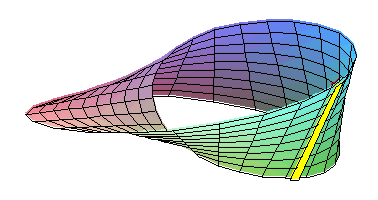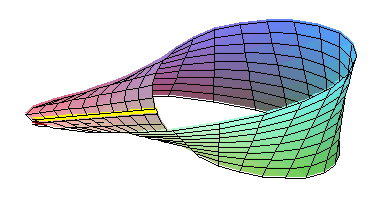
Si le matériau est élastique, il n'y a pas de problème particulier et la situation est claire. Un bâton se déplaçant comme ci-dessus décrit le ruban de Möbius. Le milieu de ce bâton décrit sans à-coup un cercle pendant qu'il tourne jusqu'à faire 180° au bout d'un tour complet. Lorsque le milieu du bâton a fait un tour, le bâton a seulement fait un demi-tour.

Cependant, lorsque la bande utilisée n'est pas extensible, comme c'est la cas pour une bande de papier, la ligne ( précédemment le cercle ) disparaît et devient une courbe irrégulière qui ressemble d'ailleurs plus à une ellipse qu'à un cercle. La plus grande partie de la torsion ne s'effectue pas de façon homogène mais trouve place en quelques petites régions distinctes du ruban. Plus la largeur du ruban est grande, moins la forme générale est circulaire et plus les contraintes de torsions sont marquées. Les mathématiciens avaient jusqu'à maintenant faits des descriptions approximatives de cette situation, mais aucune formule exacte n'avait été donnée.

Réalisé dans un matériau qui n'est pas élastique, le ruban de Möbius adopte la forme ci-dessus. Les zones rouges sont les régions à forte concentration de contraintes de torsion, alors que les régions bleues sont faiblement sollicitées.
Starostin et matériaux de Van der Heijden /Nature

« C'est un vieux problème  » rappelle l'ingénieur mécanicien Evgueni Starostin de  University College London. « C'est une question très simple, mais il s'avère qu'il exige une théorie suffisamment bonne » pour la résoudre. Starostin et son collègue Gert Van der Heijden ont maintenant trouvé la solution et ils ont publié leurs résultats en ligne dans la rubrique " Matériaux " de la revue Nature.

La forme du ruban dépend de la la largeur du papier. Plus elle est grande, plus le ruban prend une forme triangulaire qui est la forme obtenue par autorecouvrement.
Starostin et matériaux de Van der Heijden /Nature


Ils ont résolu le problème en considérant que le papier était une bande de métal résistant à la torsion et flexible. Ils ont montré que la forme du ruban de Möbius était celle qui exigeait une quantité minimale pour se plier. Des chercheurs ont été intéressés par ces recherches pour une meilleure compréhension de la torsion de l'hélice d'ADN qui tout comme le papier, ne s'étirera pas. Le ruban de Möbius a servi de modèle simplifié pour développé une technique de calcul de formes possibles prisent par l'ADN.

Billet entièrement rédigé d'après la note de Julie J.Remeyer + liens : ICI

S'il vous prend une envie pressente de crocheter un ruban de Möbius, c'est ICI

Et pourquoi ne pas agrémenter votre jardin avec cette jolie structure ?

Des mathématiques pour modéliser les eaux souterraines , une  vidéo  d'Interstices : ICI

Modélisation et simulation, une vidéo d'Interstices : ICI

Après avoir regroupé dans un même agrégateur xFruit, les flux RSS disponibles français concernant les mathématiques ( APMEP, SABIX, Blogs, EDUCNET, Café Pédagogique, Actumaths ... ), ce sont les boutons Orange en haut à droite du blog, j'ai maintenant regroupé dans un même agrégateur xFruit, des sources anglaises et américaines ( ScienceDaily et MathTrek pour le moment, j'augmenterai ce flux au fur et à mesure des flux mathématiques que je parviendrai à isoler). C'est le bouton RSS violet ci-après et en haut à droite de ce blog. Je l'ai nommé  " Actualités Mathématiques II ( anglais) ".