En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies. Ces derniers assurent le bon fonctionnement de nos services. En savoir plus.
A partir du 1er décembre et jusqu'au 24, je publierai chaque jour sur mon blog Maths au LEG, une vidéo mathématique extraite de "Advent Calendar 2006".
Vous pouvez les retrouver directement sur le site avec les explications associées :
Les mathématiciens aiment colorier. Peut-être n'ont-ils pas eu le temps de le faire à l'école, alors ils rattrapent le temps perdu.
Dès 1852, l'un d'entre eux se demanda combien il fallait de couleurs pour colorier tous les pays de n'importe quelle carte sans que deux pays voisins n'aient la même couleur. Le problème est capital car dans le cas contraire on ne pourrait plus distinguer ces deux pays après coloriage. Il pensa que quatre devait être suffisant. Beaucoup de mathématiciens prirent aussi leurs crayons de couleurs et se mirent d'accord sur le nombre : 4 doit convenir mais ils ne s'accordèrent qu'à moitié sur la preuve car celle-ci faisait intervenir un bien étrange "personnage": un ordinateur. Bref après quelques guéguerres internes sur le style, l'incontournable boite aux quatre crayons nécessaire pour colorier toutes les cartes planes imaginables de l'univers s'appelle désormais "Théorème des quatre couleurs".
Malgré la difficulté de la preuve et des conversations qui lui étaient associée, les mathématiciens s'ennuyaient un peu. C'est ainsi qu'en 1950, un certain Edward Nelson, agé de seulement 18 ans, lança un autre coloriage encore en vogue pour les occuper.
D'un air sans doute amusé, il soumit à la communauté, le petit problème suivant :
Combien faut-il de couleurs différentes pour colorier chaque point du plan, de façon que deux points distants d'une unité n'aient pas la même couleur?
Si les mathématiciens étaient troublés, ce n'était pas parce qu'ils se demandaient avec quel type de crayon ils allaient réaliser cet étrange travail mais plutôt pourquoi est-ce qu'ils avaient seulement réussi à démontrer qu'il fallait au moins 4 couleurs et au plus 7 pour réaliser cette activité presque manuelle? Ils ne parvenaient pas à donner le nombre exact de couleurs minimal dont ils avaient besoin pour colorier les points du plan avec cette contrainte: 4,5,6 ou 7?
Alors d'où vient la difficulté? Certainement de la théorie des ensembles à laquelle on peut adjoindre différentes versions de l'axiome du choix ou au contraire l'en priver.
L'axiome du choix dit qu'il est possible de prélever des éléments d'ensembles différents et de construire un autre ensemble. Si l'idée parait simpliste lorsque les ensembles sont finis, elle ne l'est pas lorsqu'ils deviennent infinis.
Bertrand Russel, nous donne une vague idée de ce que peut-être l'axiome du choix au quotidien :
Pour choisir une chaussette plutôt que l'autre pour chaque paire d'une collection infinie, on a besoin de l'axiome du choix. Mais pour les chaussures, ce n'est pas la peine.
Explication :
Cet axiome du choix est vraiment un élement trouble-fête. Il avait déjà permis à un étrange mathématicien peu scrupuleux de s'enrichir.
Il s'est aussi mis sur le chemin de deux mathématiciens Soifer et Shelah qui parvinrent à démontrer qu'en utilisant deux versions différentes de cet axiome, il fallait pour résoudre le même problème de coloriage, soit 2 couleurs, soit une infinité! C'est le grand écart.
Tout cela pour vous dire que les mathématiciens ont vraiment des "gros problèmes de coloriage"!
Inspiré de - Coloriages irréels - Complexités de Jean-Paul Delahaye aux éditions Pour la Science
Pour compléter sur l'axiome du choix :
Du choix dans la dissection - sur le blog Choux romanesco et intégrale curviligne
J'ai toujours été en difficulté devant le fait d'évaluer des travaux d'élèves sans un barème précis. Je me suis toujours aussi senti très géné lorsqu'il faut évaluer une compétence globale, différencier l'évaluation en fonction des profils des élèves et de leurs objectifs. Je suis souvent le témoin de progrès sensibles, d'efforts importants, qui ne sont pas immédiatement suivis d'effets dans les résultats d'évaluation en classe, ou au contraire de relachements de concentration, de travail, de régularité.
Comment donner un instrument de mesure aux élèves autrement que celui d'attendre la note de la prochaine évaluation en classe afin qu'ils puissent infléchir leur résultats ou de plaquer une souvent trop artificielle note de devoir maison?. Faire un devoir maison tout seul ne peut-il pas être une compétence, même si celui-ci est raté, alors qu'un camarade l'a fait faire par un prof particulier, par un parent ou a demandé de l'aide sur un forum?
Je ne sais pas si j'ai résolu la question mais j'ai fait un pas, ce qui me parait déjà pas mal. J'ai utilisé un système d'évaluation dynamique qui m'a produit une note, comme tout système d'évaluation d'ailleurs! J'ai décidé de remettre le compteur à 0 à la fin de chaque trimestre afin qu'il produise une autre note. J'ai injecté cette note dans la moyenne de chaque élève. Celle-ci est souvent plus forte que la moyenne de l'élève sauf pour quelques élèves ( environ 15% dans ce premier essai ).
C'est l'écart entre la note moyenne du trimestre et cette note ainsi que son évolution sensible dans un temps court qui lui confère son caractère dynamique. Pour quelques élèves il peut y avoir plus de cinq points d'écart en plus ou en moins par rapport à la moyenne brute. Cette note ne fait visiblement jamais passer un élève en dessous de la moyenne, ce qui me semble important et c'est souvent l'écart insuffisant entre la note dynamique et la moyenne brute qui ne permet pas de passer au dessus de la moyenne.
Je n'ai pas fait le tour des possibles mais on peut avoir l'idée de faire un mois "participation", où la participation de chaque élève est comparée, en prenant en compte leur caractèreou non, un mois "régularité du travail personnel", évaluer des travaux facultatifs etc...
J'ai pour ma part, cassé l'évaluation traditionnelle des travaux maison en faisant apparaitre des espèces de blocs de compétences qui changent en fonction de la nature du devoir et de l'année. En début d'année, j'ai plus appuyé ma notation sur la présentation, les justifications, la rédaction que sur le contenu mathématique. En fin de trimestre, j'ai évalué dans le devoir maison suivant, la capacité des élèves à produire la bonne conclusion, ainsi que celle à bien poser le problème.
Il est aussi possible de remarquer un progrès sensible sur un comportement, dans la rédaction d'un devoir, ou dans la concentration en classe. Si l'on dispose d'un blog, on peut repérer et valoriser les plus actifs participants.
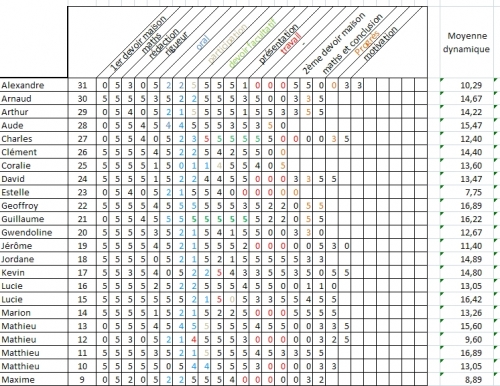
L'idée est simple à mettre en oeuvre: il suffit d'affecter à chaque élève un certain nombre de cellules d'un tableur que l'on peut compléter par des nombres de 0 à 5. Ces nombres correspondent à la compétence évaluée. Il suffit de calculer la moyenne de ces notes. Ainsi à chaque instant apparaît un indicateur que l'élève pilote au quotidien par ses actions.
La formule de la moyenne est simple :
=SOMME(Plage de données )/(5*nombre de cellules non vides de la plage de données)*20
Le nombre de cellules non vides d'une plage de donées se calcule avec la formule =nb(plage de données)
On obtient ainsi un tableau pour le premier trimestre comme suit, qui s'actualise automatiquement dès que l'on remplit l'une des cellules:
(Les intitulés sont des exemples)
Il est possible de remplir en fin de trimestre quelques cellules par une valeur afin de noter la faiblesse ou l'importance du nombre de notes. J'avais pensé donner un coefficient différent en fonction du nombre de notes mais je n'ai pas retenu l'idée car celle-ci s'avérait trop difficile à mettre en oeuvre et injuste.
J'apprécie le caractère spontané de cette technique d'évaluation qui permet de plus une différenciation possible entre les élèves lors de la notation et lors de l'interprétation des résultats.
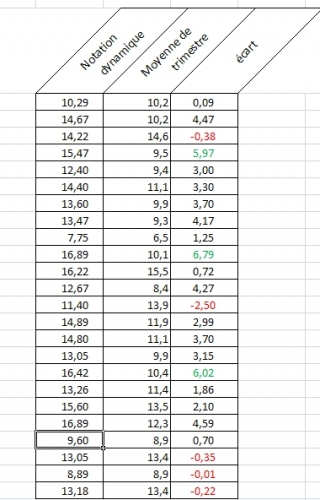
J'ai dressé pour quelques élèves le tableau comparant les deux notes, celle du trimestre et celle dynamique, la note de trimestre ayant été corrigée avec la note dynamique ( coefficient 1 pour 7 au total ).
On voit par exemple que pour deux des élèves, la différence entre cette note et leur moyenne est telle, qu'elle leur a certainement permis de passer la barrière psychologique de la moyenne!
Nous sommes en 1867, à l'Académie des sciences. Le très respectable mathématicien Michel Chasles, éponyme de la relation , bien connu de tous les lycéens, porte à la connaissance de cette illustre assemblée des lettres de Pascal à Newton, présentant des résultats dont l'origine avait été attribuée à ce dernier. Et si l'anglais Newton avait été un plagiaire de Pascal le français!
Deux ans de débats acharnés suivirent à l'Académie des Sciences opposant les partisans de l'autenticité des documents et ceux s'insurgeant devant cette mascarade.
L'affaire s'internationalise lorsque le supposé plagiaire pourrait bien être Anglais, que les Anglais rigolent de l'affaire Outre-Manche et que des lettres qui auraient été écrites par Galilée, à l'époque où celui-ci est supposé aveugle, apparaissent.
A chaque attaque en règle des défenseurs de Newton, un écrit arrive pour leur couper l'herbe sous le pied, d'autant plus que la droiture intellectuelle de Monsieur Chasles ne peut être facilement remise en cause...
Le livre de Jean-Paul Poirier " Mystification à l'Académie des sciences " aux éditions Le Pommier est à dévorer. Je viens de le finir. Il n'y a pas de passages techniques, juste le récit d'une histoire étonnante dont on a bien du mal à penser qu'elle ait pu réellement se produire tant les faits semblent inconcevables.
Pas moins de 27 000 pièces furent vendues en 7 ans par un certain Vrain-Lucas à Michel Chasles ce qui correspond à une production par ce faussaire d'exception de plus de 10 pièces par jour, dimanches et fêtes compris.
Je vous engage à vous plonger dans ce livre de 137 pages pour savourer pleinement ce récit surprenant.
J'avais parlé ici, il n'y a pas longtemps, du site Image des mathématiques, développé par le CNRS. Il est alimenté par des chercheurs qui ont le souci de vulgariser les mathématiques auprès d'un large public. Le sous-titre est "La recherche mathématique en mots et en images".
Les articles sont classés suivant le niveau du public cible, ce qui me semble être un grand pas en avant ,de considérer que la vulgarisation se veut par essence graduelle, et que tout le monde ne peut pas tout lire, ce qui à mon avis, a été l'un des écueils sur lesquels a buté l'impossible récente diffusion des sciences dures, autrement que par le coté "sensationnel" de telle ou telle avancée. Les niveaux mathématiques des articles sont répertoriés suivant les couleurs des pistes de ski ( vert, bleu, rouge et noir ).
Le site est vraiment agréable à parcourir. Il est suffisamment simple pour ne pas s'y perdre et les portraits des mathématiciens vulgarisateurs donnent beaucoup de vie à l'ensemble.
J'ai été tout particulièrement sensible aux billets de la rubrique "Café des Maths" rédigés par François Sauvageot, plus que souriant, origamis à la main. L'image des mathématiques douloureuses et laborieuses, sélectives et noires doit impérativement être cassée et ces chercheurs sont les seuls à pouvoir en donner l'impulsion et l'énergie. Beaucoup de retard a été accumulé en la matière pour réconcilier un public traumatisé, avec une recherche vivante et foisonnante. Je reste convaincu que la vulgarisation mathématique dont l'un des axes doit être entièrement dirigé vers les enseignants ( et les politiques) ne peut que dynamiser cette discipline qui peine à trouver sa place dans l'enseignement actuel.
Comme toute question mérite d'être posée, les plus grands scientifiques doivent être convaincus que toute réponse, même à une question simple, mérite d'être donnée. Les niveaux de réponses doivent être gradués suivant le public visé. L'exemple de l'objet du mois est à ce titre, très intéressant puisqu'il présente un cadran solaire digital, qui donne l'heure correcte après qu'il ait été orienté correctement. De l'enfant de 7 ans au chercheur de haut niveau, les interrogations peuvent être nombreuses et évidemment pas de la même nature!
J'ai donc été heureux de voir apparaître, dans ce café, des titres d'articles qui me "parlent", et ci c'est le cas pour moi, ça doit aussi "causer" à d'autres! :
Règle de Trois
Espérance de vie
Vulgarisation
Sudoku
Classement
Partage
On retrouve sur ce site quelques grands noms comme Etienne Ghys, Jean-Pierre Kahane et d'autres mathématiciens dont le nom ne m'est pas encore connu mais que je l'espère se piqueront au jeu de la diffusion de leurs difficiles et théoriques travaux vers un large public.
Je voulais aussi en passant, signaler l'alimentation continue du site http://www.bibnum.education.fr/ qui vise à diffuser des textes fondamentaux de la science en les faisant analyser par les scientifiques d'aujourd'hui. J'y vois un triple intérêt, d'une part de montrer l'existence de tels textes, ensuite de faire un lien entre science qui se fait et l'histoire de la science et dernièrement de permettre une analyse solide et distanciée de textes fondateurs, dont la contextualisation n'est pas facile à faire.
Si l'on se dirige sur le site Bibnum aujourd'hui, on y voit apparaître la fabuleuse tablette babylonienne YBC 7289, analysée par Benoit Rittaud qui nous fait découvrir l'incroyable précison avec laquelle les scribes ont fait leur calcul, sur ce qui était peut-être un brouillon d'élève!
Juste au dessous de cette tablette apparaît un texte de Pierre de Fermat donnant une méthode pour la recherche du minimum et du maximum, prémisse à notre bien connu calcul de dérivées. Sur la droite , le texte du jour est un texte de Stainville sur l'irationnalité du nombre e.
De quoi passer un dimanche "mathématique" bien au chaud.