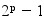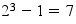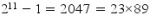J'ai assisté mercredi à la journée des maths 2008 organisée à la Faculté des Sciences à Bourges dont le thème principal était " L'expérimentation en mathématiques ".
Après l'ouverture de cette journée par les officiels, Daniel Perrin débuta sa conférence sur "L'expérimentation en mathématiques". On peut retrouver les éléments de cette riche prestation sur sa page personnelle.
On pourra noter au passage quelques " Maximes à la Daniel " :
Un des intérêts de l'expérience, c'est de se rendre compte que le problème est difficile
ou bien
En mathématiques, comme dans les autres les sciences, si l’on utilise l’expérience, elle doit être menée sérieusement.
suivie de :
Si une preuve n’est pas rigoureuse, on court le risque qu’elle soit fausse et, pire, que le résultat annoncé soit faux.
ou encore celle-ci, qui déborde heureusement largement le cadre de l'expérimentation en mathématiques:
On peut avoir une idée fausse sans pour autant être stupide.
On pourra regarder tout particulièrement l'une des situations parmi toutes celles qui sont traitées. Elle est adaptable à presque tous les niveaux d'enseignements. Il s'agit de la somme de n entiers naturels consécutifs ( page 15 puis page 26 ).
Au passage Daniel Perrin a égrené quelques extraits de "Récoltes et semailles" d'Alexandre Grothiendieck et nous a appris que même dans le milieu très fermé de la recherche mathématique le titre d'une publication: Le schéma de Hilbert est presque jamais connexe peut se transformer en: Le schéma de Hilbert est toujours connexe.
Après le repas, j'ai suivi la conférence de Bertrand Hauchecorne, non pas sur l'histoire des mathématiciens, ni sur les maths et les mots mais sur les contre-exemples.
Je ne ferai pas ici de résumé de la conférence ( mes notes sont ( très ! très ! ) incomplètes ) mais préciserai juste avoir découvert l'existence d'une curieuse et "simple" bijection de IR vers IR continue en 0 dont l'application réciproque est discontinue en 0 au milieu de nombreuses autres curiosités mathématiques mettant à rude épreuve notre intuition.
Ce fut ensuite la pause et je me suis dirigé vers l'excellente conférence de Benoit Rittaud ( sans ses notes ) sur les suites de Fibonacci aléatoires qui réservent bien des surprises et des difficultés à ceux qui souhaitent percer leurs mystères.
Si beaucoup connaissent la suite de Fibonacci "classique" : on obtient un terme en faisant la somme de ses 2 prédécesseurs, le processus étant initialisé avec les 2 premiers termes égaux à 1 ce qui donne: 1 ; 1 ; 1+1=2; 1+2=3; 2+3=5.... etc, la suite Fibonacci aléatoire s'obtient en lançant une pièce de monnaie à partir du calcul du troisième terme si c'est "pile" on fait la somme des deux précédents ( donc on ne change pas le calcul par rapport à la situation classique), par exemple 1 et 1 donnent 2 mais si l'on obtient face on fait la différence des deux prédécesseurs et plus exactement la différence en valeur absolue, c'est à dire toujours positive. 1 et 1 donneraient dans ce cas 1-1 =0.
Pour résumer si l'on obtient que des "pile" on a la suite classique : 1 1 2 3 5 8 13 21 ... et si l'on a que des "face" on obtient la sute suivante: 1 1 0 1 1 0 1 1 0 1 1 0 ...
Et entre les deux... et justement le problème est là : que se passe-t-il entre les deux? Certaines propriétés sont connues "en moyennant", d'autres restent encore dans l'ombre. La conférence de Benoit Rittaud, en vidéo, vient d'être mise en ligne récemment ICI ( consulter la visionneuse pour le texte et visualiser les arbres ).
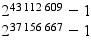
 Un nombre premier est un nombre divisible par 1 et par lui-même, comme 3, 5 , 7....
Un nombre premier est un nombre divisible par 1 et par lui-même, comme 3, 5 , 7....