Un 45ème nombre de Mersenne premier peut-être découvert
 Un nombre premier est un nombre divisible par 1 et par lui-même, comme 3, 5 , 7....
Un nombre premier est un nombre divisible par 1 et par lui-même, comme 3, 5 , 7....
Un nombre de Mersenne est un nombre entier de la forme:
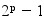
avec p premier :
Les nombres de Mersenne fournissent de bons candidats pour les nombres premiers.
Par exemple pour p=3, le nombre de Mersenne vaut
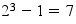
et il est premier.
Mais pour p=11, le nombre de Mersenne vaut
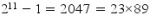
et n'est pas premier.
En fait, l'humanité n'a pour l'instant trouvé "que" 44 nombres premiers de Mersenne, leur avantage étant qu'ils produisent les plus grands nombres premiers connus. Voilà le tableau des nombres de Mersenne connus à ce jour. Le plus grand est colossal et possède 9 808 358 chiffres.
| # | p | Mp | Chiffres | Découverte | Découvreur |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | Antiquité | Inconnu |
| 2 | 3 | 7 | 1 | Antiquité | Inconnu |
| 3 | 5 | 31 | 2 | Antiquité | Inconnu |
| 4 | 7 | 127 | 3 | Antiquité | Inconnu |
| 5 | 13 | 8 191 | 4 | XIIIe siècle | Ibn Fallus |
| 6 | 17 | 131 071 | 6 | 1588 | Cataldi |
| 7 | 19 | 524 287 | 6 | 1588 | Cataldi |
| 8 | 31 | 2 147 483 647 | 10 | 1750 | Euler |
| 9 | 61 | 2 305 843 009 213 693 951 | 19 | 1883 | Pervushin |
| 10 | 89 | 618970019…449562111 | 27 | 1911 | Powers |
| 11 | 107 | 162259276…010288127 | 33 | 1914 | Powers |
| 12 | 127 | 170141183…884105727 | 39 | 1876 | Lucas |
| 13 | 521 | 686479766…115057151 | 157 | 30 janvier 1952 | Robinson (Swac) |
| 14 | 607 | 531137992…031728127 | 183 | 30 janvier 1952 | Robinson (Swac) |
| 15 | 1 279 | 104079321…168729087 | 386 | 25 juin 1952 | Robinson (Swac) |
| 16 | 2 203 | 147597991…697771007 | 664 | 7 octobre 1952 | Robinson (Swac) |
| 17 | 2 281 | 446087557…132836351 | 687 | 9 octobre 1952 | Robinson (Swac) |
| 18 | 3 217 | 259117086…909315071 | 969 | 8 septembre 1957 | Riesel (Besk) |
| 19 | 4 253 | 190797007…350484991 | 1 281 | 3 novembre 1961 | Hurwitz (IBM) |
| 20 | 4 423 | 285542542…608580607 | 1 332 | 3 novembre 1961 | Hurwitz (IBM) |
| 21 | 9 689 | 478220278…225754111 | 2 917 | 11 mai 1963 | Gillies (Illiac) |
| 22 | 9 941 | 346088282…789463551 | 2 993 | 16 mai 1963 | Gillies (Illiac) |
| 23 | 11 213 | 281411201…696392191 | 3 376 | 2 juin 1963 | Gillies (Illiac) |
| 24 | 19 937 | 431542479…968041471 | 6 002 | 4 mars 1971 | Tuckerman (IBM) |
| 25 | 21 701 | 448679166…511882751 | 6 533 | 30 octobre 1978 | Noll & Glenn (CDC) |
| 26 | 23 209 | 402874115…779264511 | 6 987 | 9 février 1979 | Noll (CDC) |
| 27 | 44 497 | 854509824…011228671 | 13 395 | 8 avril 1979 | Nelson & Slowinski (Cray Research) |
| 28 | 86 243 | 536927995…433438207 | 25 962 | 25 septembre 1982 | Slowinski (Cray) |
| 29 | 110 503 | 521928313…465515007 | 33 265 | 28 janvier 1988 | Colquitt & Welsh (Nec) |
| 30 | 132 049 | 512740276…730061311 | 39 751 | 19 septembre 1983 | Slowinski (Cray) |
| 31 | 216 091 | 746093103…815528447 | 65 050 | 1 septembre 1985 | Slowinski (Cray) |
| 32 | 756 839 | 174135906…544677887 | 227 832 | 19 février 1992 | Slowinski & Gage |
| 33 | 859 433 | 129498125…500142591 | 258 716 | 10 janvier 1994 | Slowinski & Gage |
| 34 | 1 257 787 | 412245773…089366527 | 378 632 | 3 septembre 1996 | Slowinski & Gage |
| 35 | 1 398 269 | 814717564…451315711 | 420 921 | 13 novembre 1996 | GIMPS / Joel Armengaud |
| 36 | 2 976 221 | 623340076…729201151 | 895 932 | 24 août 1997 | GIMPS / Gordon Spence |
| 37 | 3 021 377 | 127411683…024694271 | 909 526 | 27 janvier 1998 | GIMPS / Roland Clarkson |
| 38 | 6 972 593 | 437075744…924193791 | 2 098 960 | 1er juin 1999 | GIMPS / Nayan Hajratwala |
| 39 | 13 466 917 | 924947738…256259071 | 4 053 946 | 14 novembre 2001 | GIMPS / Michael Cameron |
| 40* | 20 996 011 | 125976895…855682047 | 6 320 430 | 17 novembre 2003 | GIMPS / Michael Shafer |
| 41* | 24 036 583 | 299410429…733969407 | 7 235 733 | 15 mai 2004 | GIMPS / Josh Findley |
| 42* | 25 964 951 | 122164630…577077247 | 7 816 230 | 18 février 2005 | GIMPS / Martin Nowak |
| 43* | 30 402 457 | 315416475…652943871 | 9 152 052 | 15 décembre 2005 | GIMPS/ Cooper & Boone |
| 44* | 32 582 657 | 124575026…053967871 | 9 808 358 | 4 septembre 2006 | GIMPS/ Cooper & Boone |
Lorsque l'exposant p commence à devenir important, il est nécessaire d'avoir recours à l'ordinateur, et même d'utiliser plusieurs ordinateurs. C'est ce que fait le projet GIMPS depuis 1996 où l'on constate dans le tableau précédent que ce mode de calcul a permis de découvrir les 10 derniers nombres premiers de Mersenne et donc les plus grands nombres premiers connus à ce jour.
Il semblerait qu'un 45ème nombre de Mersenne ait été découvert par GIMPS.
Mon ordinateur est associé à ce projet. par exemple en ce moment, mon ordinateur teste le nombre M39760033. C'est peut-être grâce à moi qu'a été découvert un 45ème nombre premier, ce 23 août. Si c'est le cas, j'espère qu'une partie des $100 000 de récompense me reviendra mais j'ai comme un doute...
En plus le propriétaire était en vacance ( pas moi ) celui de GIMPS... donc la validation du résultat devra attendre la mi-septembre.
On August 23rd, a computer reported finding a new Mersenne prime to the server! Because I was on vacation, verification did not begin until the 26th. Two verification runs are in progress. Estimated completion is September 12th and September 16th. Check back here for updates!
L'article de Scientific American:
World record ($100,000) prime number found?