Inadvertance numérique
Cela fait de nombreuses années que je publie sur support numérique, sur des blogs, des wikis, que j'utilise les possibilités du web 2.0. Cela fait plus de deux ans que je dispose d'un ENT dans mon établissement que je voyais se réduire à deux utilisations principales: publier les notes en ligne et recopier mon cahier de texte papier en ligne, ce qui représentait pour moi, un travail que je jugeais fastidieux (j'oserai même dire presque inutile!). Mais en fait, je viens de faire une découverte naïve en ce début d'année...
Le cahier de textes est un support numérique et il accepte donc le code HTML. Et là, ça change tout, car je peux publier et embarquer ce que je souhaite.
J'ai été surpris de cette découverte tardive, que je juge naïve, compte tenu du nombre d'heures que je passe à écrire en ligne et à m'occuper des possibilités de publication numérique. Toujours est-il que je n'avais pas fais le lien entre ma publication numérique sur mes blogs, wikis et autres sites et la publication numérique en HTML sur l'ENT.
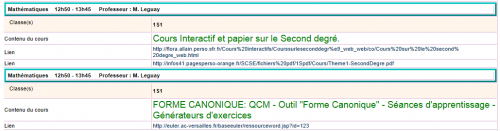
Voilà donc quelques copies de mon cahier de texte... version numérique avec:
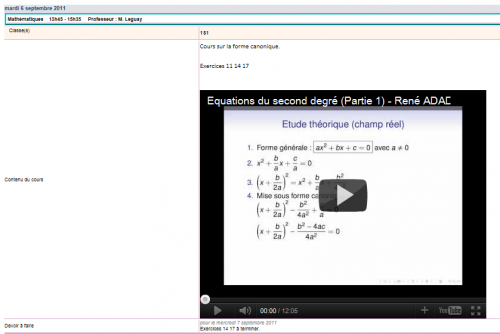
Des vidéos:
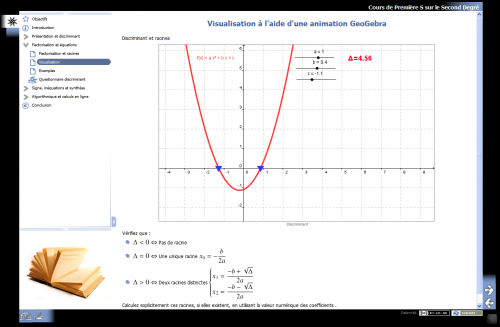
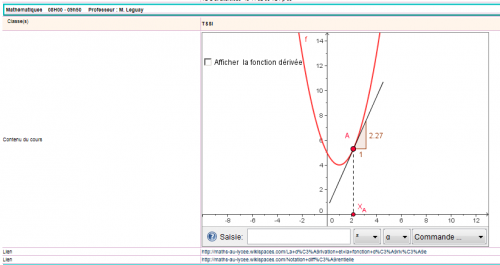
Des applets GeoGebra manipulables:
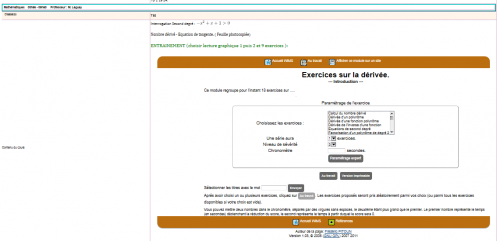
Du code HTML par exemple celui de Wims
Des hyperliens:
Des caractères mathématiques:
La naïveté n'est sans doute pas à associer à cette découverte. Je pense qu'il faut plus se tourner vers le fait que la publication numérique est composite et fait intervenir des ressources et des compétences diverses. Jusqu'à maintenant, j'ai eu la vision fausse qu'il était important de convertir l'ensemble de mes documents vers un même format, vers un même support. C'est sans doute possible mais je ne pense pas que ce soit d'un grand intérêt. En fait la puissance du numérique provient de sa souplesse, de son acceptation presque sans limites de multiples formes, sources et formats numériques. Et cela est rendu possible en manipulant très rapidement quelques lignes de code HTML!... Révolutionnaire.


 Au début du XXème siècle,
Au début du XXème siècle,