Discriminons OPALE Sup
J'ai découvert On m'a fait découvrir OPALE Sup. C'est en fait le logicel que je cherchais depuis bien longtemps, ne sachant pas qu'un tel produit existait. Il s'agit d'une chaine éditoriable libre, permettant éditer des cours sur supports numériques ainsi que des éditions papier.
OPALE fonctionne avec Open Office et supporte un moteur LATEX pour l'édition des caractères mathématiques.
J'ai produit un cours sur le second degré de Première S, incluant une vidéo (humoristique), des animations GeoGebra, des caractères mathématiques, des images et des codes d'embarquement d'applets, des exercices (type QCM et QCU).
Je crois que j'arrive ici au stade final que je m'étais fixé dans l'édition numérique. Je trouvais déjà que le wiki de l'année passée était une grande avancée.
OPALE est très stable et ne plante pas. La consultation des premiers tutoriels permet de le prendre en main rapidement et cela est facilité d'autant plus que l'on a une certaine pratique de l'édition numérique. La création d'un tel cours est longue (3 jours environ), non parce que c'est difficile mais simplement parce que les opérations et les écritures sont nombreuses.
Je n'ai rencontré quasiment aucun inconvénient pendant l'utilisation si ce n'est le fait de ne pas voir le code HTML des applets, ni leur exécution lorsqu'on le recopie. C'est un problème bien mineur compte tenu de la grande qualité du logiciel.
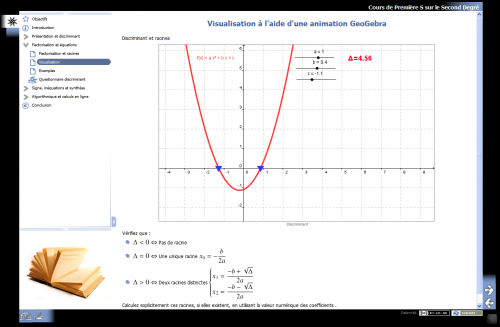
Vous pouvez voir le résultat ICI.
Le logiciel fournit une édition papier ODT. Elle peut-être remise en forme. Les vidéos et les applets n'y apparaissent pas. Les adresses des hyperliens sont renvoyées en note de bas de page. Je vous livre la version du chapitre sans modification ICI.

Commentaires
Pas sûr que le (la?) St Louis Gateway Arch ait une forme parabolique...
http://www.karakas-online.de/forum/viewtopic.php?t=935
Idem pour le/la St Louis Abbey :)
Effectivement. En plus j'ai ouvert la page! http://www.jug.net/wt/arch.htm
http://www.inclassablesmathematiques.fr/archive/2010/11/09/les-constructions-les-plus-mathematiques-du-monde.html
Visiblement rien de parabolique. Par contre pour la chapelle, j'avais trouvé cette source : http://mathtourist.blogspot.com/2009/07/st-louis-parabolas.html
Je vais modifier l'exemple.
Merci
C'est modifié. Je vais enrichir le contenu au fur et à mesure mais je me suis occupé, pour débuter, plus de la forme que du fond, car c'est plutôt ce point qui m’intéressait au départ avec la maîtrise du logiciel et la transposition numérique (médiatisation).
Encore merci pour le retour.
De rien!
Effectivement, c'est la prise en main du logiciel qui importe en premier lieu!
Bonjour,
sacré belle trouvaille. Pas trop dure la prise en main ? car moi aussi c'est ce que je cherche et je n'ai pas envie de perdre trop de temps à comprendre le process !!
Il existe en libre deux générateurs d'e-learning:
Opale sup et exe-learning
Exe-learning est beaucoup plus convivial et le résultat final meilleur
Malheureusement la communauté universitaire française soutient Opale sup et ne s'intéresse pas du tout à exe-learning
Si vous souhaitez voir des réalisations faites en exe-learning et une avec Opale
http://formav-lms-e-learning.fr/newslearning/realisations-de-formav
Merci, je vais tester de suite.
excellent : je cherchais un exemple en mathématique du secondaire de l'utilisation d'opale
par contre deux remarques amicales :
1) dans le test "questionnaire canon" la questions 3 est infaisable sans la forme canonique dont tu parles
2) dans l'animation geogebra sur le signe du trinome, il n'y a pas de portion "verte" sur la courbe lorsque x_1 >x_2
mais en tout cas chapeau pour l'effort .. il ne reste plus qu'à m'y mettre
cordialement
M. Gras, enseignant en lycée