J'ai terminé la partie initiale du wiki "Maths au lycée" ( fonctionnant sous Firefox et Internet Explorer + MathPlayer). Celui-ci est destiné aux élèves de lycée. La partie que j'ai rédigée comprend des synthèses de cours qui sont dans la plupart des cas illustrées par des animations GeoGebra ou ce sont elles qui en constituent l'élément central. J'ai volontairement omis de préciser s'il s'agissait de définitions ou de théorèmes (lorsque c'était possible! C'est par exemple difficile de parler du théorème des gendarmes sans utiliser ce mot ou de donner la définition des suites adjacentes sans le mot "définition"). J'ai aussi choisi d'utiliser parfois le langage courant pour expliquer certaines notions et préciser quelques méthodes et pièges sans vraiment les distinguer du contenu mathématique pur.
J'ai terminé la partie initiale du wiki "Maths au lycée" ( fonctionnant sous Firefox et Internet Explorer + MathPlayer). Celui-ci est destiné aux élèves de lycée. La partie que j'ai rédigée comprend des synthèses de cours qui sont dans la plupart des cas illustrées par des animations GeoGebra ou ce sont elles qui en constituent l'élément central. J'ai volontairement omis de préciser s'il s'agissait de définitions ou de théorèmes (lorsque c'était possible! C'est par exemple difficile de parler du théorème des gendarmes sans utiliser ce mot ou de donner la définition des suites adjacentes sans le mot "définition"). J'ai aussi choisi d'utiliser parfois le langage courant pour expliquer certaines notions et préciser quelques méthodes et pièges sans vraiment les distinguer du contenu mathématique pur.
En fait l'idée est de considérer que la synthèse de cours sera utilisée par les élèves, soit en ligne (façon Zapping) pour ses animations, retrouver celles qui ont été vues en cours, avec la possibilité de visualiser les mathématiques de façon dynamique en manipulant les applets, soit imprimée, le paramétrage des animations pouvant être réalisé dans cet objectif et les pages pouvant (et devant) être anotées par les élèves. L'impression des pages est facilement accessible par l'onglet page. Je me demande même si l'idée de fournir cette base aux élèves en cours comme support de notes ne serait pas satisfaisante. Elle pourrait être considérée comme élément transitoire entre la connaissance inconnue à acquérir et la connaissance présentée sous sa forme finalisée et structurée.
J'ai placé les progressions envisagées à coté des cours pour faire "coller" le contenu du wiki au vécu des élèves, tout en évitant le piège de la numérotation en chapitres qui ne permet guère de modifications ultérieures, ne serait-ce que pour l'adapter aux réformes qui se succèdent.
J'ai aussi choisi de ne placer aucune démonstration dans cette synthèse pour plusieurs raisons. Ce travail a déjà été assez long (et bénévole!). Les démonstrations auraient fait perdre le caractère synthétique du projet et elle ne demandent guère d'être animées. L'idée est donc d'une part de les replacer comme élément fondateur dans le cours en classe et d'essayer d'impliquer les élèves dans leur rédaction sur le wiki. J'avais déjà tenté l'expérience il y a deux ans sur le wiki-blog et je vais la renouveler à la rentrée prochaine sur ce wiki. J'ai choisi un petit gif sympa pour lier les démonstrations à la synthèse animée qui me parait assez bien ilustrer la situation:
Pour les liens externes et internes, j'ai choisi mon infatigable oiseau :
L'objectif exclusif que je vais me fixer l'année prochaine sera de faire tourner ce wiki sur trois classes: Première S, Terminale ES et Terminale S. Ce sera sans connexion Internet. Les animations Geogebra seront présentes sur un portable relié à un vidéo-projecteur. Je pense commencer l'année en fournissant aux élèves la synthèse imprimée puis me dégager de cette contrainte en la transférant vers les élèves si ils le souhaitent.
J'aurai peut-être besoin de reconduire une micro-structure type "atelier maths" si le projet ne prend pas racine en classe entière. J'utiliserai de toutes façon encore Edmodo pour la communication et le contact avec les élèves. Le wiki sera la façade externe et Edmodo en sera la composante interne.
J'ai aussi l'intention de développer des activités pédagogiques impliquant les élèves comme la rédaction de devoirs en temps libres à plusieurs mains. On peut aussi envisager l'écriture d'algorithmes et leur publication. J'ai tenté l'expérience cette année dans un petit atelier (toujours bénévole!). En moyenne quatre élèves ont été impliqués pendant 2/3 de l'année à raison d'1/2 heure par semaine. L'un d'entre eux , Alexis, a particulièrement été productif. Je n'avais pas trop orienté l'atelier vers les maths pour ne pas effrayer les quelques rares volontaires.
Il serait intéressant d'augmenter ce wiki avec les classes que je n'ai pas. Si j'ai le temps je m'y collerai mais une telle démarche pourrait être reprise par d'autres collègues, sur ce wiki ou sur un autre, dans la même optique et avec une charte graphique similaire. Je pense cependant que l'utilisation régulière d'un tel outil le condamne nécessairement à n'être collectif qu'autour d'un enseignant ou d'un groupe limité d'enseignants qui suivent les mêmes objectifs.
Lien permanent
Catégories : Constructions, Geogebra, Infos, Mathématiques, Outils web, Pour le prof de maths, Pour les lycéens, Représentations, Visuel et audio
Tags : wiki, applets, geogebra, enseignement, lycée, cours, mathématiques, mathé
2 commentaires

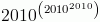 pièces de monnaie.
pièces de monnaie.