Des graphes pour mieux comprendre la conscience
Ma thèse en 180 secondes de Gaspard Fougea - Université Paris- Saclay :
Modèles formels pour la conscience : de l’expérience subjective aux algorithmes cognitifs
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies. Ces derniers assurent le bon fonctionnement de nos services. En savoir plus.
Ma thèse en 180 secondes de Gaspard Fougea - Université Paris- Saclay :
Modèles formels pour la conscience : de l’expérience subjective aux algorithmes cognitifs
Intervention d'Albert Burroni sur le thème de « Mathématique des structures de l'informatique théorique », lors de l'édition 2012 de la conférence-table ronde mathématiques innovantes.
Cette conférence sur le thème « Réseaux et structures dynamiques » s'est déroulé le Mardi 22 mai 2012 dans les locaux de Supméca Paris.
Le cours de Didier Müller d'introduction à la théorie des graphes est disponible depuis peu au format papier.
 Introduction à la théorie des graphes
Introduction à la théorie des graphes
Cahier CRM N° 6
Didier Müller
48 pages
2012
Le but de ce fascicule est d'initier les lycéens à la théorie des graphes. Il n'a pas pour ambition de présenter une théorie complète, mais de montrer comment les graphes peuvent être une méthode de résolution de problèmes intéressante.
Ce cours se veut accessible aux élèves de lycée, car il ne demande pratiquement pas de connaissances préalables. Il est découpé en deux parties principales : les graphes non orientés et les graphes orientés.
Comme la théorie des graphes utilise un jargon bien particulier, le début du cours comporte beaucoup de définitions. Un index et un lexique en fin de fascicule aideront l'élève à assimiler ces termes.
Les 75 exercices sont essentiellement de deux types :
Une version papier (sans les corrigés) peut être commandée sur le site de la diffusion Pahud. Ce fascicule est aussi disponible en ligne gratuitement, ainsi qu'un second cahier contenant les solutions détaillées des exercices.
Voilà une bonne question et si on la pose à M. Google voilà ce qu'il nous répond ou plutôt ce que les principaux utilisateurs de forums nous répondent.
Bon allez, en fonction de la tête du joueur, de l'âge de celui qui répond et ses connaissances tennistiques on voit apparaître les noms de Nadal, de Federer, de Börg, de Mac Enroe, Wilander, Edberg et cela seulement en consultant le premier lien précédent.
J'ai toujours révé de me faire interroger sur la question par un vrai journaliste sportif. Ah, tiens je le vois arriver.
Le journaliste sportif
- Bonjour, vous êtes Webmaster des Inclassables Mathématiques et passionné de tennis.
Moi
- C'est ça oui.
Moi (dans ma tête)
- J'adore qu'on m'appelle Webmaster avec un W majuscule.
Le journaliste sportif
- Alors pour vous quel est le meilleur joueur de tennis de tous les temps?
Moi
- Personnellement, je dirai Jimmy Connors à cause de ça:
Le journaliste sportif
- Je vois qu'en fait vous êtes très attaché à Connors car c'est un excellent showman mais objectivement, rationnellement, rien ne vous permet de dire que Jimmy Connors est le meilleur joueur de tous les temps.
Moi (dans ma tête)
- Le journaliste ne doit sans doute pas savoir que je suis prof de maths et que je peux apporter des arguments mathématiques et rationnels.
Moi
- Il faudrait en fait que je vous explique comment faire une analyse du réseau complexe de l'histoire du tennis professionnel depuis 1968 mais je ne sais pas si vous vous sentez d'attaque (de coup droit bien sûr).
Rires (en plus je fais rire le journaliste sportif, je suis aux anges...)
Moi
-Alors allons-y.
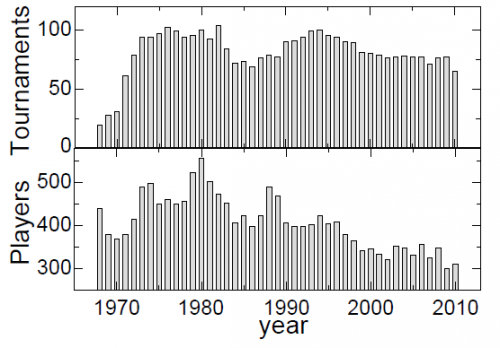
Nous allons tout d'abord définir les conditions de l'analyse. Nous prendrons en compte les résultats de tous les matchs joués par les joueurs de tennis professionnels entre 1968 et 2010. Tous les matchs du Grand Chelem et ceux intervenant dans le classement ATP seront pris en compte, soit au total 3700 joueurs, 3640 tournois et 133 261 matches.
Si le nombre de tournois est assez régulier avec cependant des pics en 1980 et 1992 avec plus de 90 tournois par an, le nombre de joueurs ne cesse de décroître linéairement depuis 1996 et est passé de 400 environ à 300, comme l'indique le graphique suivant:
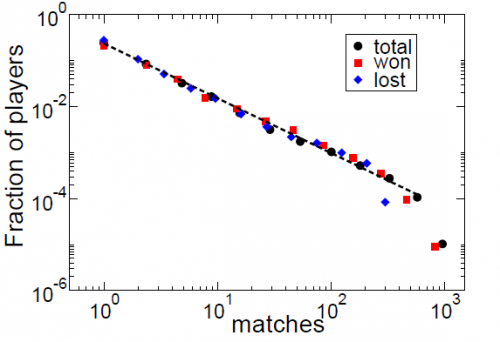
Le graphique suivant indique la proportion de de joueurs ayant remporté ou perdu un nombre donné de matches. On voit que beaucoup de joueurs gagnent ou perdent peu de matches (en fait ils quittent les tournois rapidement. A l'autre bout, un petit groupe de joueurs (les meilleurs) jouent beaucoup de matches qu'ils gagnent généralement contre les plus faibles et aussi entre eux qu'ils gagnent ou qu'ils perdent, connu sous le nom d'effet Matthew (les pauvres deviennent plus pauvres et les riches plus riches).
Nous allons ensuite construire le graphe des rencontres. Il sera orienté (une flèche sera "tracée" à chaque victoire du joueur j vers le joueur i) et pondérée par le nombre de défaites du joueur j contre le joueur i.
Le graphique suivant est un sous-graphe extrait de celui de tous les joueurs concernant ceux qui ont été premier au classement ATP. L'intensité et la largeur d'une flêche sont proportionnelles au logarithme de son importance (poids).
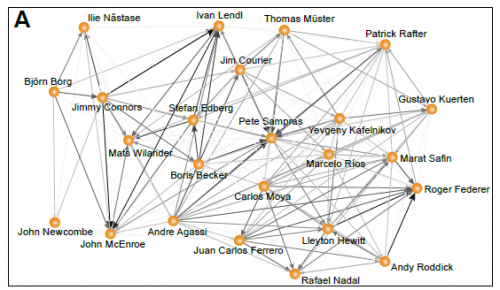
La représentation de ce résau peut être utilisée pour classer les joueurs en calculant pour chacun leur taux de "Prestige" dont la somme serait égale à 1. Celà n'est pas sans rappeler la méthode de calcul du PageRank pour classer les pages Web.
Le prestige d'un joueur i représente la fraction de prestige totale de l'état d'équilibre du graphe dans un processus de diffusion. Pour expliquer en termes un peu plus simples, chaque nouveau résultat d'un matche modifie le "prestige" des deux compétiteurs puis par diffusion celui de tous les joueurs. Les mathématiques nous indiques que ce calcul converge vers un équilibre permettant de calculer le nouveau "Prestige" de tous les joueurs du graphes. Par exemple un joueur k qui a gagné contre le joueur i qui vient lui même de remporter un matche contre un adversaire fort voit son prestige augmenter.
Comme dans le cas du PageRank, il est nécessaire de fixer la valeur d'un paramètre (c pour le PageRank, q ici). La valeur a été choisie dans les deux cas.
Le graphique suivant indique le prestige en fonction du nombre de victoires (jusqu'à 7) pour différentes valeurs du paramètre q. Le choix de 0.15 est "traditionnel" et équilibré.
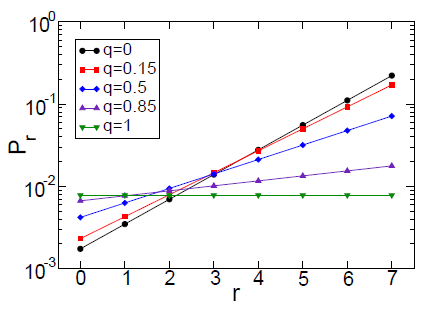
Plus le nombre de matchs gagné est grand plus le prestige est grand. Cependant, le nombre de match gagnés augmentant, le niveau de prestige doit être recalculé en implémentant une condition dite de normalisation, imposant qu'une quantité donnée soit constante. Elle permettra ainsi de définir un Prestige de référence a partir duquel tous les autres pourront être caculés. Cette condition impose que la somme des produits du nombre de victoires par le prestige pour chaque joueur soit égal à 1.
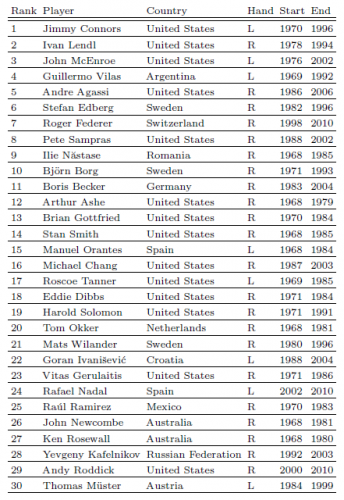
Et le résultat est bien celui que je vous avais donné. Jimmy Connors est bien le meilleur joueur de tous les temps:
Le journaliste sportif
- C'est certainement aussi celui qui a gagné le plus grand nombre de matches, c'est à dire dont la carrière a été la plus longue. Et les joueurs dont la carrière est terminée sont favorisés par rapport aux autres qui sont en cours de carrière. Alors pour ce qui est de la rationnalité de votre méthode de calcul permettez moi d'en douter.
Moi (un peu embarassé par les arguments du journaliste)
- Burp, c'est à dire que en fait... Vous voyez, il ne faut pas confondre le nombre de victoires et le prestige. Rafael Nadal par exemple serait classé 40 ème au nombre de victoires alors qu'il est à la 24 ème position dans notre classement. C'est aussi visible pour Björn Borg qui a eu une carrière plus courte que la moyenne et est cependant classé dans le top 10 de notre classement.
Pour ce qui est de la carrière en cours d'un certain nombre de joueurs, vous avez remarqué qu'il y a un biais. On peut penser à un classement annuel qui diffère parfois du classement ATP et IDF.
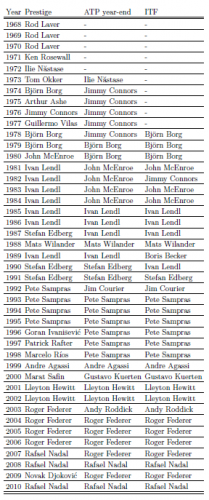
Il est possible aussi de penser à un classement par type de surface qui donnerait Jimmy Connors gagnant pour l'herbe et Andre Agassi pour les surfaces dures. Si l'on considère le meilleur joueur des tournois en terre battue c'est Guillermo Villas.
En faisant le calcul par décennie, Jimmy Connors est le meilleur pour les années 70, Ivan Lendl pour les années 80, Pete Sampras pour les années 90 et Roger Federer pour les anées 2000.
Le classement par "Prestige" est donc une nouvelle forme de classement qui ne coïncide d'ailleurs pas toujours avec les classements techniques et qui permet en outre de faire des comparaisons sur des temps longs.
Le journaliste sportif
- Merci, je crois que j'ai tout compris, enfin la partie non technique. Vos inclassables mathématiques ont prouvé leur incroyable efficacité et ont eu raison de mes inclassables joueurs de tennis.
Moi
-Si vous voulez de plus amples informations sur la partie technique de ces classements, je vous renvoie à l'article original de Filippo Radicchi publié sur ArXiv. Voilà c'est fini.
Une petite page de blog sympa pour lier les graphes et les dessins : ICI