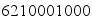Vous êtes né le 26 janvier 1847 et vous voulez savoir si 2601 ou 1847 sont des nombres particuliers.

Vous aviez oublié que 6969 était strobogrammatique

et que 4511 = 4444 + 55 + 11 + 1.

What's special about this number? vous rafraîchira la mémoire.

Il y a aussi une très bonne façon de s'informer sur les nombres entiers en parcourant les deux pages de liens de Wikipédia intitulées "Catégorie nombres entiers".

On pourra ainsi trouver le premier nombre premier strobogrammatique.

Ou bien s'apercevoir que 6210001000 est le seul nombre autodescriptif en base 10.
Et qu'est-ce qu'un nombre auto descriptif?
Rien de plus simple c'est un nombre qui se décrit lui-même en base 10 ?

Et pourquoi se décrit-il lui même en base 10 ?

Monsieur Darcos n'a-t'il pas parlé d'autonomie? Alors je vous laisse chercher un peu ( ce n'est pas difficile!) et si personne ne laisse la réponse en commentaire, c'est promis, je vous aiderai.

Alexandre Moatti en avait parlé il y a déjà 7 mois sur Maths 2.0 et le projet vient de se concrétiser.

BibNum est un projet de bibliothèque numérique de textes scientifiques antérieurs à 1940, commentés par des scientifiques contemporains qui souhaitent partager leur intérêt pour ces textes et analysent leur impact dans la science et la technologie actuelle.

A ce jour 13 textes sont disponibles. Le fonctionnement du site est simple et efficace puisqu'une fenêtre SCRIBD s'ouvre pour permettre la lecture et l'édition du texte commenté par une personnalité scientifique. Un flux RSS ( devenu indispensable!) est  présent pour se tenir informé des nouveautés. Il y a même des tags !

Pour connaître la liste des textes ayant un rapport avec les mathématiques, il suffit donc de consulter le tag "mathématiques".

Au programme purement mathématique :

Mémoire sur les conditions de résolubilité des équations par radicaux
Auteur :Evariste Galois (1811 - 1832) - Analyse par Caroline Ehrhardt

Bonne lecture.

C'est à peu près en ces termes que se traduit la pensée des spécialistes de la finance et aussi de  Benoit B. Mandelbrot lorsqu'il parlait des marchés financiers. Les modèles standards utilisés prévoient beaucoup trop de variations moyennes et presque aucune forte variation. Or les marchés boursiers sont soumis à de très fortes variations comme on peut le constater en ce moment.

Un article rédigé par Mandelbrot en 1999 sur ce sujet dans Scientific American a été publié de nouveau en raison de l'actualité. On le trouvera ICI ( c'est en anglais!).

Il est intitulé " Comment les fractales peuvent expliquer ce qui est faux à Wall Street "
La géométrie qui décrit la forme des littoraux et les modèles de galaxies élucide aussi comment les prix des actions montent en flêche et chutent.

Je ne peux que vous conseiller de lire en complément à ce sujet, le livre de Walter et Levy Vehel, publié en 2002 " Les marchés fractals" qui aborde ce problème en profondeur.

Aurait-on pu confier le théorème de Fermat à un groupe d'Enarques qui nous auraient fait des directives, des super-directives ? Y seraient-ils arrivés en 300 ans? C'est impossible, il faut des idées!

Jean-Yves Girard (au sujet du formalisme en mathématiques - 19.45)

Une excellente conférence pleine d'humour.

• Introduction
• 10:10L'arithmétique de Peano
• 06:34Mathématique v.s informatique
• 12:20Paradoxes
• 04:40Les formalistes
• 10:58Imcomplétude
• 08:28Intuitionnismes
• 11:08Questions

Une mise en boite géante pour le 1500ème post de ce blog :