C'est Bézout me crie-t-on dans les oreilles pas Bezout !
Tout ceux qui font la spé maths en TS le savent ( je ne la fais pas, c'est vrai !) on dit le théorème de Bézout et pas de Bezout!
Oui sauf que voilà, j'ai habité 30 ans près de Nemours et d'Avon communes de naissance et de décès de notre mathématicien au nom mystérieux.
Alors depuis quelques temps, je cherche d'où peut bien venir l'hésitation, car hésitation il y a !
A Nemours, personne ne prononce Bézout. Tout le monde dit Bezout ( mais qui le connait?). Aucun enseignant du lycée ne prononce Bézout ( j'ai demandé à l'un d'entre eux). Ce n'est d'ailleurs pas si clair que ça ,car voilà ce que l'on trouve en première page du site du lycée :
A l'adresse suivante :
Lycée Etienne Bezout
31 avenue Etienne Dailly
77140 Nemours
Et puis je cherche sur Google la rue Bezout à Nemours, il doit bien y en avoir une. Bien sûr qu'il y en a une, je la connais. Et bien non, Google nous indique une rue Bézout :
Agrandir le plan
Mais non je vous jure, à Nemours il n'y a pas de rue Bézout mais une rue Bezout. Regardez par vous-même la photo que j'ai prise :

Je vous l'avais bien dit, c'est une rue Bezout à Nemours. Les majuscules ne prennent pas d'accent me direz-vous, c'est pour ça.
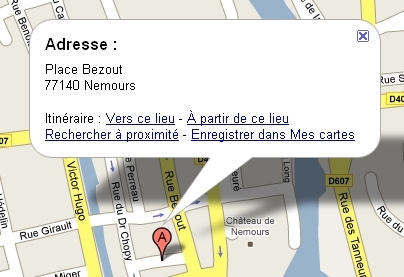
Je me souviens aussi d'une place Bezout à Nemours alors je cherche sur Google, place Bézout comme pour la rue, et qu'est-ce que je trouve?
Qu'il n'existe pas de place Bézout à Nemours mais qu'il existe bien une place Bezout, juste à coté de la rue Bézout. Vérifiez par vous-même :
De plus en plus étrange...
Mais que disent les matheux de tout ça ?
Dans "L'Epreuve d'exposé au CAPES Mathématiques - Volume III" publié en 2007 par Dany-Jack Mercier, voilà ce que l'on peut lire en réponse à la question Qui était Bezout? ( sans é ):
Etienne Bézout (et oui, on devrait dire "Bézout", mais les deux écritures sont admises)....
Mais on n'a toujours aucun renseignement au sujet de la double orthographe.
Les Archives Départementales de Seine et Marne mentionnent Bezout, seule orthographe qui semble y être connue ( j'ai téléphoné).
Au Ministère de la Culture c'est Bezout
Poursuivons notre enquête en nous tournant vers un livre original de l'auteur :

Ah oui, la majuscule est bien accentuée, il doit donc bien s'agir de Bézout et non de Bezout. Mais alors d'où proviennent ces deux orthographes? Mystère...
Terminons notre enquête avec Wikipédia qui nous montre une photo de la pierre tombale où le texte présente de petites majuscules accentuées mais ne fait pas apparaître d'accent sur le "E" du nom, écrit quant à lui, en grandes majuscules.
Et vous au fait, vous dites Bézout ou Bezout ?