Prix Nobel de la Paix 2007 : Le GIEC - mieux comprendre l'apport de la France
Une chronologie des évènements:
Juin 2005 : La terre se réchauffe plus que jamais.
Absents lors du dernier rapport du GIEC, les chercheurs français de l’IPSL et de Météo-France viennent de présenter les premiers résultats obtenus à partir de leurs deux nouveaux modèles climatiques. Conclusion : la Terre va se réchauffer, y compris lorsque les émissions de CO2 seront stabilisées.
Pour tenir compte de ces facteurs, ce ne sont pas moins de onze scénarios que les deux modèles français ont testés.
Le premier, dit de référence, simule un climat « non perturbé », celui du début du XIXe siècle, avant la révolution industrielle. Le second correspond à l’évolution du climat au cours du XXe siècle (de 1860 à 2000) : il doit permettre de mieux comprendre comment les différents facteurs (gaz à effet de serre, aérosols sulfatés, modification de la constante solaire et volcanisme) ont contribué à l'évolution du climat sur cette période.
Tous les autres scénarios correspondent à des projections pour le XXIe siècle ou au-delà. Certains privilégient une croissance démographique et économique rapide (scénarios de type A), d’autres considèrent que des mesures environnementales vont être prises (scénarios de type B), avec transferts de technologie* (type 1) ou sans (type 2). On comparera ainsi le scénario le plus pessimiste, A2 (« on ne fait rien »), au plus optimiste, B1 (« on met en œuvre des mesures draconiennes contre les émissions de gaz à effet de serre »). Plus original, les chercheurs ont également cherché à savoir comment évoluerait le climat si les émissions de CO2 pouvaient être stabilisées.
22 600 heures ( 2 ans et demi ! ) de calculs pour Météo-France, 20 000 heures pour l’IPSL… comme pour toutes les modélisations climatiques, les résultats français ont nécessité des temps de calculs considérables.
Dans tous les scénarios : la Terre se réchauffe
L'intégralité de l'article : ICI
Les résultats de l'Institut Pierre Simon de Laplace : ICI
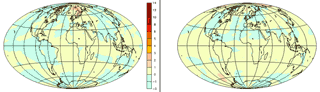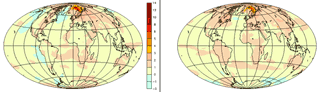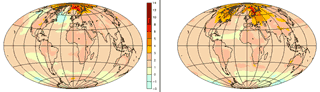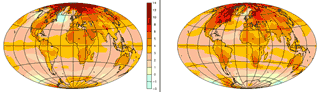
Comparaison de 2 modèles Météo-France et IPSL pour le scénario A2 : ICI
Janvier 2007 : Le livre blanc des nouvelles simulations climatiques françaises.
La communauté climatique française publie le 31 janvier 2007 un Livre blanc sur de nouvelles analyses des simulations climatiques françaises dont une partie a contribué à la préparation du prochain rapport du Groupe d’experts Intergouvernemental sur l’Evolution du Climat (GIEC).
L'intégralité de l'article : ICI
L'américain Al Gore et le GIEC, le panel d'experts sur l'évolution du climat se partagent le Prix Nobel de la Paix. Ancien vice-président de Bill Clinton et candidat démocrate malheureux à la Maison Blanche en 2000, Al Gore, est revenu sur le devant de la scène l'an dernier avec son livre et documentaire "Une vérité qui dérange". Primé deux fois aux Oscars, le film contribue à vulgariser un sujet complexe et à sensibiliser l'opinion publique à la menace climatique.
Le prix Nobel de la Paix leur est décerné conjointement "pour leurs efforts de collecte et de diffusion des connaissances sur les changements climatiques provoqués par l'homme et pour avoir posé les fondements pour les mesures nécessaires à la lutte contre ces changements", a expliqué à Oslo le président du comité Nobel norvégien, Ole Danbolt Mjoes. Le GIEC est le groupe d'experts intergouvernemental sur l'évolution du climat, un organisme chapeauté par l'ONU et présidé par l'indien Rajendra Pachauri.
Ses rapports fournissent un solide socle de connaissances aux décideurs politiques. L'attribution du Prix Nobel de la Paix à Al Gore et au GIEC lance un signal fort à la communauté internationale à quelques semaines de la conférence de Bali.
Cette conférence qui se tiendra début décembre doit tracer la feuille de route pour de nouveaux engagements de réduction des émissions de gaz à effet de serre au-delà de 2012, après l'expiration de la première phase du protocole de Kyoto.
Le prix Nobel de la Paix sera remis le 10 décembre, à la date anniversaire de la mort d'Alfred Nobel. Les lauréats recevront une médaille d'or, un diplôme et un prix d'une valeur de 10 millions de couronnes suédoises, soit environ 1,08 millions d'euros.
Source Euronews : ICI
Les lanceurs d'alerte du GIEC, 11 questions à la climatologue Valérie Masson-Delmotte, co-auteur du 4ème rapport du GIEC : ICI
Le portail français du GIEC : ICI
L'homme responsable du réchauffement ? et Comment va la banquise aujourd'hui. Deux vidéos du CNRS : ICI et ICI et plus généralement le PODCAST du CNRS : Alerte aux pôles : ICI
Giec : le rapport est prêt et le réchauffement… officiellement irréversible, l'article de FuturaSciences : ICI
Tous les articles du blog sur le sujet ( dont celui-ci) : ICI

 Décidément, Archimède se retrouve propulsé à la Une des Inclassables, hier effacé, aujourd'hui... inutile !
Décidément, Archimède se retrouve propulsé à la Une des Inclassables, hier effacé, aujourd'hui... inutile !