Cliquer sur l'image pour découvrir le site en espagnol

Cliquer sur l'image pour l'agrandir.

L'Ecole d'Athènes est une fresque réalisée par le peintre Raphaël entre 1509 et 1510. L'oeuvre fait près de 8 mètres de large sur 2,5 mètres de hauteur.

Cette fresque symbolique présente les figures majeures de la pensée antique. Les personnages sont représentés en des places et des postures particulières, ornés de certains attributs, ce  qui permet d'en identifier certains. Ils sont disposés sur deux lignes horizontales principales, et sont séparés par une verticale nettement discernable, ce qui confère à ce tableau ordre et symétrie parfaite.  L'Ecole d'Athène représente un haut lieu de culture philosophique, dont l'humanisme transpire d'ailleurs du tableau, qui s'oppose à la culture théologique. Le cadre architectural est classique. On ne peut s'empécher d'y voir le souvenir des termes romains. Cet environnement fait contrepoid aux univers mythologiques souvent présents dans les tableaux de Raphaël. Le regard du spectateur se dirige en premier lieu vers le centre du tableau où se tiennent debout les deux personnages principaux: Platon (14) et Aristote (15) , majestueux et habillés de la toge romaine. Platon tient le Timée, et pointe le doigt vers le haut pour montrer que la connaissance procède d'un mouvement ascendant, qui va de la terre au ciel de l'idéal philosophique, alors qu'Aristote,  dirige la paume de la main vers le sol indiquant que tout idéal philosophique ne peut exister que dans le monde d'ici-bas.

Tous les personnages sont référencés dans l'article de wikipédia. Il semble qu'il y ait quelques doutes sur l'identité de certains d'entres eux. Nous nous arréterons dans cette note à la seule composante "mathématique" des figurants de cette fresque

Une lecture dynamique de cette fresque est possible ICI . On y voit en particulier les éléments de perspective, d'éclairage et la présence du nombre d'or ( rectangles et carrés ) au centre de la scène. Une étude des éléments de perspective du tableau est disponible ICI.

La première question qui vient à l'esprit est Y a-t-il des maths dans le Timée que tient Platon à la main? ( que j'espère tout le monde a lu !).

La réponse vient sans se faire attendre puisque s'il n'y a pas de mathématiques pures dans le Timée ( le problème du doublement de la surface d'un carré se trouve par exemple dans le Ménon ), il y a bien la présence des quatre solides réguliers de l'espace sur cinq,  dit d'ailleurs de Platon. Les mathématiciens de l'époque connaissaient leur existence. Ces joyaux géométriques sont formés à partir des trois polygones réguliers suivants: le triangle équilatéral, le carré et le pentagone régulier donnant naissance en les rapprochant dans l'espace autour d'un sommet aux cinq polyèdres suivants: le tétraèdre (chaque sommet voit trois triangles équilatéraux) , l'octaèdre (chaque sommet voit quatre triangles équilatéraux), l'icosaèdre (chaque sommet voit cinq triangles équilatéraux), le cube (chaque sommet voit trois carrés), et le dodécaèdre (c'est celui qui manque et chaque sommet voit trois pentagones réguliers). En fait une fois l'existence de ces merveilleux objets établie, montrer qu'il n'en existe pas d'autres est très simple puisqu'il suffit de constater que si l'on place  six triangles équilatéraux dans un plan autour d'un sommet commun on occupe la totalité des 360° disponibles et on ne peut pas les replier dans l'espace. Il en est de même avec un sommet qui verrait quatre carrés de 90°, ce qui remplit aussi l'espace. Quatre pentagones ayant un sommet commun se recouvrent déjà dans le plan, impossible donc de les replier dans l'espace pour former un volume!

Le recherche d'harmonie est sous-jacente à la construction de cet univers tridimensionnel parfait et si le triangle équilatéral et le carré sont à son origine, c'est parce que ces deux figures peuvent être formée à partir des éléments "atomiques" de la géométrie que sont les triangles rectangles. Un triangle équilatéral peut se concevoir en juxtaposant  deux triangles rectangles dont les deux cotés adjacents à l'angle droit mesurent la moitié l'un de l'autre, mais c'est une construction encore plus harmnieuse que choisira de présenter Platon dans le Timée qui utilise non pas deux mais six triangles rectangles. Il est aussi possible de former un carré à partir de deux triangles rectangles isocèles. Il devient ainsi plus aisé de comprendre pourquoi le dodécaèdre formé à partir de pentagones réguliers ( qui ne peuvent se construirent à partir de triangles rectangles ) a été découvert plus tardivement. On notera sans doute la forte influence pythagoricienne dans ces raisonnements.

Tout ceci est remarquablement illustré, expliqué et apparait sous forme animée sur le site IcosaWeb dans une page intitulée "Les corps platoniciens "

Mais l'objectif de Platon était en fait de mettre ces quatre volumes parfaits en relation avec le monde d'en bas ( Platon associera l'éther au dodécaèdre plus tardivement), et si vous avez parcouru la page précédente, vous n'avez pas pu manquer le fait que ces quatres corps de base ont été associés à deux éléments dont l'existence est garantie par le toucher et la vue: la terre et le feu et deux éléments "nécessaires" pour garantir deux moyens proportionnels: eau et l'air. L'idée est encore atomiste, les quatre éléments sont les briques insécables à partir desquelles peut se construire (penser) le Monde de façon harmonieuse. André Ross explique cela très bien dans l'article suivant intitulé "Mathématiques et civilisation" ainsi que dans Platon et les mathématiques".

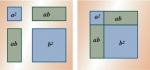Si l'on considère que la figure de référence du plan est le carré dont chaque coté peut être partagé dans un rapport a et b.  Trois "nombres-surface" suffisent pour recomposer le carré : aa, ab et bb.

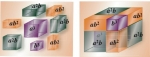Alors que si l'on découpe un cube dans les mêmes proportions, il faut quatre "nombres-volume" et donc quatre éléments ( or l'univers est bien tridimentionnel!) : aaa, abb, aab, bbb et le fait qu'ils soient en proportion géométrique garantira l'harmonie de la construction!

On a donc bien présent dans le Timée la première équation mathématique modélisant le monde. Les mathématiques aparaissent comme le langage intermédiaire permettant de faire le lien entre le monde d'en bas imparfait et périssable et le Ciel des Idées parfait et intemporel :

Dans ce livre, en pointant son doigt vers le ciel, c'est ce message que Platon envoie au monde terrestre et qui, je le pense, reste encore bien présent de nos jours.

La seconde question qui peut-être intéressante est de savoir quels sont, dans ce tableau, les personnages ayant un rapport privilégié avec les mathématiques?

On trouve peut-être en 1, Zénon d'Elée qui est à l'origine  des premiers paradoxes de type "mathématique". On se rappellera d'Achille qui ne peut pas rejoindre la tortue et de la flèche qui n'atteint jamais son but. - (Diaporama)

En 6, il s'agit de Pythagore (VIème siècle avant J.C.) dont le nom est très connu mais dont le personnage possède encore beaucoup de mystères, historiques d'une part et sur qui qu'il était vraiment.

En 9, Hypatie première femme mathématicienne connue au destin tragique, apparaît peut-être sous les traits de Francesco Maria I^er della Rovere.

En 18 Euclide ou Archimède pourraient être représentés sous les traits de Bramante, maître et protecteur de Raphaël.

Les principaux représentants antiques des mathématiques ( sauf Thalès ) semblent donc présents, certes sous d'autres traits, mais c'est aussi le cas pour Platon qui a prit les traits de Léonard de Vinci pour l'occasion.

En ce qui concerne Pythagore, on pourra consulter les liens suivants afin de mieux connaître cet homme prédicateur, qui fonda une communauté religieuse et politique composée exclusivement d'hommes vétus de blancs fuyant les femmes en couche, qui évitent de rentrer dans la maison d'un mort, refusent de croquer une fève ou de manger un oeuf, qui doivent respecter la règle du silence et une discipline stricte tout en exaltant le courage et l'honneur du combat. En fait la communauté est partagée entre deux attitudes correspondant à celles des deux leaders. Il y a d'un coté les adeptes de Pythagore, le mage ascète, replié sur lui, retiré de la cité, inquiet de toutes les formes d'impuretés qui pourrait faire obstacle au salut de l'âme et de l'autre, les pythagoriciens "politiques" qui suivent Milon de Crotone son gendre, mangent de la viande, acceptent le monde de la cité avec l'intention d'agir sur lui pour le transformer .

Pythagore fut le premier à envisager le nombre sous une perspective religieuse et mystique, libérant au passage les mathématiques de leur seule visée utilitaire à laquelle ils étaient cantonnés jusque là et c'est cette forme de pensée qui a résisté au temps. (Universalis ).

Pour compléter sur Pythagore:

Les diaporamas d'André Ross

Pythagore, la géométrie des nombres

Pythagore, des triplets au théorème

Pythagore, moyennes et proportions

Pythagore par l'Encyclopédie de l'Agora

Pour un rappel de la contribution de Pythagore dans l'histoire des mathématiques : La brève histoire des mathématiques

A noter : J.-F. Mattei : Pythagore et les pythagoriciens (Que sais-je n° 2732)

On pourra aussi lire le passage pittoresque suivant sur les purgations physiques et spirituelles d'André Dacier, philologue né en 1651 dans La vie de Pythagore, ses symboles; La vie de Hiéroclès et ses vers dorés:

L'anamorphose est un procédé connu depuis bien longtemps. Regarder un dessin anamorphique sous un angle qui ne convient pas revient par exemple à voir cela :

Et mathématiquement tout s'explique dans Miroirs et perspectives

En 1478, il y avait 84 ateliers d'ébénisterie à Florence s'occupant principalement de marqueterie. Les marqueteurs étaient nommés les maîtres de la perspective.

C'est vers les années 1450 que la marqueterie évolua de simple décor architectural secondaire à la position éminente d'art géométrique par excellence. A cette époque, les panneaux de marqueterie représentaient souvent des scènes urbaines vues comme au travers d'une fenêtre ouverte. Certains panneaux représentaient aussi de façon saisissante le contenu d'un buffet dont les portes seraient entrebâillées. Ils éaient parfois composés de plus d'un millier de pièces découpées avec une extrême précision dans des essences de bois diverses ( ébène, cyprès, buis, noyer ) après qu'eut été réalisé un dessin en perspective et que l'aspect naturel de certains morceaux ait été modifié par teinture ou apr brûlage superficiel afin de renforcer l'effet de profondeur.

Les deux théoriciens de la perspective qui permirent l'essor de cet art étaient Florentins. Il s'agissait de Filippo Brunelleschi et de Leon Batista Alberti.

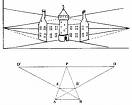
C'est Alberti qui fut à l'origine de ce que l'on appelle aujourd'hui le point de fuite et la ligne d'horizon. C'est lui aussi qui représenta le premier la grille figurant un plancher carrelé dont les figures diminuent avec l'éloignement.

Depuis le moyen-âge, s'affrontaient les partisans de l'extramission qui affirmaient que l'oeil envoyait de rayons lumineux et ce ceux de l'intramission qui pensaient au contraire que les rayons provenaient des objets pour se diriger vers l'oeil. Les  théoriciens médiévaux des deux camps se sont accordés sur.... le rayon central, celui par lequel le monde est le mieux perçu et symbole de la moralité divine. Alberti n'avait pas besoin de pencher dans l'un ou l'autre camp puisque sa pyramide de vision, à la base de sa théorie, gardait la même géométrie quelque soit le sens du rayon. Le sommet de cette pyramide coïncidait avec l'oeil et sa base avec ce qu'il voyait.

Avec cette formulation, la construction des oeuvres possédait une base théorique tout aussi solide que celle élaborée par les Pythagoriciens 550 ans avant JC sur la musique et perpétuée jusqu'alors par le quadrivium de la scolastique.

Peindre ou représenter le monde visible devenait alors le moyen d'étudier les lois de la nature et l'on comprend à quel point il était nécessaire d'être le plus fidèle possible à la réalité.

Fra Giovanni de Vérone était un maître de la marqueterie de cette époque. Il réalisa le panneau suivant aux alentours de 1519. On y voit dans sa partie supérieure un polyèdre à 72 faces, symbole de l'architecture. Accrochés sous l'étagère, on trouve les instruments de marqueterie - le compas, la règle, la pièce carrée - autour desquels est  enroulé un ruban sur lequel est écrit en grec " Voici les outils de marqueterie". Sur le bas du buffet est représenté, comme posé, le mazzochio, cette structure torique en boudin, qui était à la fois une coiffure florentine et un symbole de la géométrie dans l'espace.

On remarque très bien la maîtrise totale de l'artiste dans son art en regardant les panneaux suivants ( source ICI - en italien, que je vous conseille de parcourir intégralement).

ã Copyright 2001 dell'associazione l'Arengario, Monza

Les marqueteurs étaient des artistes, des géomètres et des menuisiers.

Dans beaucoup d'oeuvres, la géométrie ne figure pas comme seul moyen de conception et d'execution, mais elle est aussi au centre de la représentation elle-même. La marqueterie est ainsi un exemple assez surprenant d'autoréférence, propriété particulièrement intéressante pour les philosophie des arts, du langage et des mathématiques.

Il est intéressant de noter que Platon opposait la fausseté de l'art à la vérité des mathématiques, il résuma l'ordre, l'harmonie et l'explication du monde aux cinq solides parfaits... qui comme pour faire un pied de nez à toute son oeuvre se retrouvent au centre des représentations artistiques. La possibilité qu'ont les artistes à les représenter augmentant la compréhension qu'ils ont de ces objets et du monde,

C'est certainement dans la figure du mazzochio, que s'unissaient symboliquement les mathématiques et les ats picturaux. La construction de cette figure était considérée comme très difficile jusqu'à la fin du XVème siècle. Pour les marqueteurs le mazzochio était certainement le lien entre leur travail et la renaissance des mathématiques. Il était le "chef-d'oeuvre" de ces maîtres de la perspective.

Sa représentation demandait des connaissances et une technique importante en perspective. En effet, avant d'arriver à la figure finale, il fallait itérer un processus complexe pour l'époque.

La première étape consistait à construire deux octogones  symétrique par rapport à une verticale, puis a tracer les horizontales joignant leurs sommets.

La deuxième étape consiste à construire les polygones concentriques que l'on voit sur la figure ci-dessus ( cliquer sur la figure pour ouvrir le fichier PDF et agrandir l'image page 2).

La troisième étape permet de reporter les points obtenus par projection des cercles sur la figure de l'étape 1 comme on le voit très bien sur l'image précédente en bas à gauche.

La quatrième étape permet de construire un quadrillage adapté à le représentation dans l'espace.

La cinquième étape permet de construire une première ligne polygonale en perspective.

Le mazzochio complet est obtenu avec sept itérations successives des étapes 4 et 5. Chacune de ces itérations permet le tracé d'une ligne polygonale en perspective.

On retrouve cette figure du mazzochio représentée par Uccello dont les dessins préparatoires laissent apparaître les trous de la pointe du compas et les lignes du tracé.

On peut se laisser séduire par l'achat d'une  représentation de ce mazzochio en se rendant sur le site des musées italiens ( cliquez sur l'image ).

© MuZéO 2006 

 

Après que cet art fut porté au plus haut, son déclin n'en fut que plus fulgurant. Au XVème, Vasari, reflétant la pensée du moment déclarait que la marqueterie était pratiquée par ceux qui avaient plus de patience que de talent! Vasari pensait d'ailleurs que les travaux d'Uccello étaient une perte de temps.

Le climat artistique changea profondément et le milieu du XVIème vit l'apparition d'un Michel-Ange qui s'éleva contre une formulation trop stricte des règles de perspective.

Bientôt les mathématiques tant honorées le siècle précédent furent dénigrées avec vigueur. Zuccari rejeta même complètement l'apport des mathématiques dans la peinture.

Le désintérêt de la perspective sonna le glas de la marqueterie. En fait après 1525, les travaux de marqueterie n'étaient plus réalisés que d'après des cartons sans grande valeur artistique, les marqueteurs devenant ainsi de pâles imitateurs de peintures, alors qu'il avaient été à l'origine des plus grandes avancées dans le domaine de la perspective, ce qui permit au peintre de se les approprier.

Au regard de l'histoire, les marqueteurs méritent donc d'être replacés au centre de la renaissance comme ceux qui ont permis "la rationalisation de l'espace vu".

Source : Pour la Science Septembre 1982

La perspective est sans doute le domaine où les mathématiques ont montré leur face la plus artistique. Dans un article ( PDF ) nommé "L'histoire de la perspective au XXème siècle: une déconstruction": ICI , Jeanne Peiffer interroge  les liens unissant ces deux aspects de la perspective, l'un mathématique, l'autre artistique. Celle-ci ne se laissant pas facilement enfermer dans l'un ou l'autre de ces deux domaines, J. Peiffer nous emmène aux sources de l'origine, entre mythe et métaphore, certitudes et inventions.

 

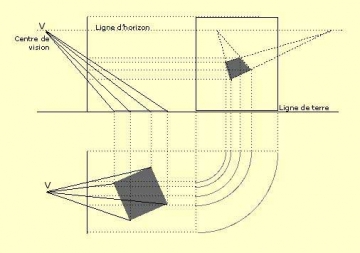
Si vous avez fait votre choix entre perspective mathématique ou perspective artistique, il faut maintenant passer aux travaux pratiques !
Pour construire une maison tout en douceur sur de la musique classique en perspective à un, puis deux, puis trois points :