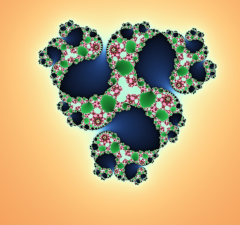
Tout le monde ou presque a déjà entendu parler de fractales. On sait généralement  que c'est un joli dessin qui peut ressembler à ça :

Et puis c'est à peu près tout. C'est déjà bien mais on peut tenter de faire mieux et de comprendre comment on obtient ces jooliiiis dessssins de fractales et avec quel logiciel libre obtenir ces images ( sur lesquelles on peut cliquer pour les agrandir).

Alors nous allons tenter de faire simple et procéder par étapes. Il suffira ensuite d'un peu d'imagination, non pas pour aller sur l'île aux enfants mais au pays, non pas celui de Candy mais des fractales.

Trèfle de plaisanterie, dit le lapin dans son carré de luzerne et revenons à nos moutons.

1) Prendre un nombre, le multiplier par lui-même et le retrancher:

Prenons 3, multiplions-le par lui même 3x3=9 et ôtons lui 3 soit 6

Prenons 4, multiplions-le par lui même 4x4=16 et ôtons lui 4 soit 12

Prenons 0.5, multiplions-le par lui même 0.5x0.5=0.25 et ôtons lui 0.5, il reste -0.25

2) Répéter l'opération:

Pour chaque nombre de départ, on répète indéfiniment la même opération.

Recommençons avec 3, la première étape donne 6, recommençons l'opération avec 6 en le multipliant par lui-même ce qui fait 36 et ôtons lui 6 ce qui nous fait 36-6=30 et recommençons jusqu'à l'infini. Il semble évident que les résultats vos devenir de plus en plus grands. On dira dans ce cas que la suite de nombres est divergente.

Prenons un autre nombre de départ, par exemple 1, on le multiplie par lui-même, on obtient 1 et lui ôte 1 ce qui donne 0. On recommence l'opération avec 0 que l'on multiplie par lui-même soit 0 et auquel on enlève 0, ce qui nous donne 0. Force est de constater que si l'on répète l'opération indéfiniment, le résultat sera toujours 0. On dira dans ce cas, puisque le résultat est un nombre, que la suite de nombres est convergente.

3) La peinture

Nous allons maintenant nous lancer dans le domaine artistique. Nous allons peindre les nombres de départ en fonction de la valeur qu'ils donnent au terme du processus répété indéfiniment que l'on vient d'énoncer précédemment. Les nombres qui sont à l'origine d'une suite convergente resteront noirs, comme le 1 ou le 0. Les autres prendront diverses couleurs, en fonction de la "vitesse" à laquelle la suite va diverger, c'est à dire  du nombre d'étapes qu'il faudra pour  faire atteindre une valeur donnée à cette suite de nombres. Si l'on regarde une droite où sont repérés tous les nombres, et si le processus est bien choisi , on devrait voir de nombreuses couleurs apparaître et des portions de droite restant noires, celles comprenant les nombres initiaux qui donnent une suite convergente.

Lire la suite