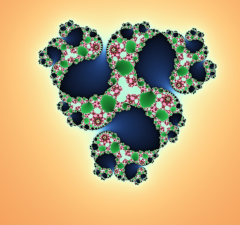
Tout le monde ou presque a déjà entendu parler de fractales. On sait généralement  que c'est un joli dessin qui peut ressembler à ça :

Et puis c'est à peu près tout. C'est déjà bien mais on peut tenter de faire mieux et de comprendre comment on obtient ces jooliiiis dessssins de fractales et avec quel logiciel libre obtenir ces images ( sur lesquelles on peut cliquer pour les agrandir).

Alors nous allons tenter de faire simple et procéder par étapes. Il suffira ensuite d'un peu d'imagination, non pas pour aller sur l'île aux enfants mais au pays, non pas celui de Candy mais des fractales.

Trèfle de plaisanterie, dit le lapin dans son carré de luzerne et revenons à nos moutons.

1) Prendre un nombre, le multiplier par lui-même et le retrancher:

Prenons 3, multiplions-le par lui même 3x3=9 et ôtons lui 3 soit 6

Prenons 4, multiplions-le par lui même 4x4=16 et ôtons lui 4 soit 12

Prenons 0.5, multiplions-le par lui même 0.5x0.5=0.25 et ôtons lui 0.5, il reste -0.25

2) Répéter l'opération:

Pour chaque nombre de départ, on répète indéfiniment la même opération.

Recommençons avec 3, la première étape donne 6, recommençons l'opération avec 6 en le multipliant par lui-même ce qui fait 36 et ôtons lui 6 ce qui nous fait 36-6=30 et recommençons jusqu'à l'infini. Il semble évident que les résultats vos devenir de plus en plus grands. On dira dans ce cas que la suite de nombres est divergente.

Prenons un autre nombre de départ, par exemple 1, on le multiplie par lui-même, on obtient 1 et lui ôte 1 ce qui donne 0. On recommence l'opération avec 0 que l'on multiplie par lui-même soit 0 et auquel on enlève 0, ce qui nous donne 0. Force est de constater que si l'on répète l'opération indéfiniment, le résultat sera toujours 0. On dira dans ce cas, puisque le résultat est un nombre, que la suite de nombres est convergente.

3) La peinture

Nous allons maintenant nous lancer dans le domaine artistique. Nous allons peindre les nombres de départ en fonction de la valeur qu'ils donnent au terme du processus répété indéfiniment que l'on vient d'énoncer précédemment. Les nombres qui sont à l'origine d'une suite convergente resteront noirs, comme le 1 ou le 0. Les autres prendront diverses couleurs, en fonction de la "vitesse" à laquelle la suite va diverger, c'est à dire  du nombre d'étapes qu'il faudra pour  faire atteindre une valeur donnée à cette suite de nombres. Si l'on regarde une droite où sont repérés tous les nombres, et si le processus est bien choisi , on devrait voir de nombreuses couleurs apparaître et des portions de droite restant noires, celles comprenant les nombres initiaux qui donnent une suite convergente.

4) La fractale de Julia

Supposons maintenant que Gaston Julia soit quelqu'un qui ait trouvé "un bon processus" permettant d'obtenir de jolies couleurs par exemple multiplier un nombre par lui-même et lui ajouter toujours le même nombre que l'on nommera c. Supposons maintenant que le nombre initial (complexe) corresponde à un point du plan. En fonction de la valeur obtenue par la répétition infinie du processus, nous allons peindre les nombres de départ avec de jooooliiies cooouuleuurs et laisser en noir ceux qui sont à l'origine d'une suite qui converge.

Voilà résultat avec c=0

On voit que tous les points à l'intérieur sont à l'origine d'une suite convergente, c'est à dire qu'en répétant indéfiniment le processus, on obtient à la fin un nombre, et que ceux qui sont à l'extérieur produisent une suite divergente dont les différentes couleurs sont associées à la façon la suite diverge. Regardons ce qui se passe vers le bord, de ce qui semble bien être un disque !

Rien de spécial, sauf qu'avec un très fort grossissement, nous voyons que les points ne sont pas colorés en orange mais en bleu. La suite obtenue avec des nombres situés juste au bord du disque ne diverge pas à la même  "vitesse", que ceux situés loin du disque. Ceci n'était pas visible sans faire un zoom sur le bord.

On peut maintenant changer la valeur de c et admirer sur un exemple, la complexité ( et la beauté) de l'ensemble de Julia.

On peut zoomer à l'intérieur de cet ensemble et constater le phénomène d'auto-similarité, c'est à dire qu'à une échelle différente, on retrouve un motif similaire au précédent.

5) La fractale de Mandelbrot

Reprenons notre transformation, la deuxième, celle qui multiplie un nombre par lui même et qui lui ajoute un nombre que nous avions nommé c. Contrairement à tout à l'heure avec Julia, nous prenons toujours le même nombre de départ pour démarrer le processus: 0 par exemple. On choisit un nombre c, qui est  associé à un point du plan et on regarde comment se comporte la suite de nombres obtenue en répétant le processus à l'infini. Si celle-ci est convergente on peint le point du plan correspondant au nombre c en noir, sinon on utilise une palette de couleurs en fonction de la façon dont la suite diverge et on obtient la star des fractales: l'ensemble de Mandelbrot !

6) Mandelbrot et ses Julia

Imaginons que l'on passe la souris sur l'ensemble de Mandelbrot, on récupère les coordonnées d'un point, ce point peut être associé au nombre c d'un ensemble de Julia. A tout point de l'ensemble de Mandelbrot correspond donc un ensemble de Julia. Ce que l'on peut voir dans  cette vidéo avec au premier plan l'ensemble de Mandelbrot, la souris qui se déplace dessus, et en bas à droite de l'écran, l'ensemble de Julia correspondant à la position de la souris.

7) Le logiciel d'exploration

Fraqtive est un logiciel extrémement simple qui permet de naviguer dans les ensembles de Mandelbrot et de Julia. C'est celui que j'ai utilisé pour faire ces images et celles de cette galerie.

Le choix d'afficher en premier plan l'ensemble de Mandelbrot ou de Julia se fait par sélection du type de fractales. sur la droite de l'écran. Si l'on est sur l'ensemble de Mandelbrot en premier plan et que l'on déplace la souris, on affiche l'ensemble de Julia correspondant en premier plan, en double cliquant sur le bouton droit. On peut zoomer et se déplacer dans les ensembles en utilisant la souris et les flêches de navigation.

On peut changer l'exposant dans la formule pour l'ensemble de Mandelbrot et donner une valeur de x et y correspondant à la valeur complexe de c pour afficher le Julia correspondant.

Fraqtive est libre et développé pour Windows, OS X et Linux.

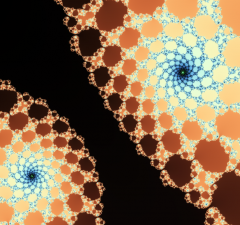
Voilà quelques images obtenues en zoomant dans la première fractale de ce billet:

Bonne visite et pour les amateurs du genre n'hésitez pas à consulter le tag fractales de ce blog.