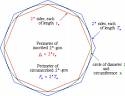
 La méthode d'exhaustion était utilisée par les mathématiciens grecs pour déterminer une longueur, une aire ou un volume. On pense à tort qu'elle est seulement constituée par un "encadrement" d'une courbe par deux lignes brisées situées de part et d'autre, d'une surface par des polygones ou d'un volume par des polyèdres, ceux-ci étant intérieurs et extérieurs. Ainsi, en " rapprochant " les objets créés de celui dont on cherche à évaluer la longueur, l'aire ou le volume, on aboutit intuitivement à un encadrement de la quantité cherchée.
La méthode d'exhaustion était utilisée par les mathématiciens grecs pour déterminer une longueur, une aire ou un volume. On pense à tort qu'elle est seulement constituée par un "encadrement" d'une courbe par deux lignes brisées situées de part et d'autre, d'une surface par des polygones ou d'un volume par des polyèdres, ceux-ci étant intérieurs et extérieurs. Ainsi, en " rapprochant " les objets créés de celui dont on cherche à évaluer la longueur, l'aire ou le volume, on aboutit intuitivement à un encadrement de la quantité cherchée.
La méthode d'exhaustion est en fait essentiellement constituée par la preuve irréfutable de cette intuition et la validation du résultat obtenu par une double réduction à l'absurde. C'est ce que nous explique à merveille André Ross dans un article ( PDF ) : ICI
Archimède utilisa cette méthode afin d'obtenir des résultats très originaux, dont un calcul d'aire faisant intervenir un " levier " pour comparer l'aire d'un triangle et l'aire d'un segment de parabole : ICI
Le résultat le plus connu est obtenu par Archimède, et est sans conteste, l'encadrement de Pi : ICI
Cette méthode, près de 2000 ans auparavant, préparait le terrain du calcul différentiel et intégral qui permettra des calculs plus généraux.
Cavalieri emprunta le chemin de ses ainés dans son Traité des indivisibles pour effectuer des calculs d'aire et de volume : ICI
La méthode de Descartes était purement algébrique, elle ne faisait pas intervenir les concepts de limite et d'infinitésimal, la route se poursuivit avec Newton et Leibnitz et la naissance du calcul différentiel et intégral.
Pour info, voilà l'adresse de la page d'André Ross avec tous les articles cités et d'autres encore : ICI
Et d'autres articles d'André Ross : ICI
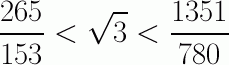
 Il existe sur le web bon nombre d'anecdotes, mais peu en français (voire pas du tout ?), et comme Boris Gourévitch est passionné par la vie des mathématiciens (serait-ce le fruit d'une frustration sous-jacente ?), il se propose de vous faire découvrir quelques-unes des histoires connues ou moins connues. Tout cela pour nous rappeler que ce sont bien des hommes eux aussi !
Il existe sur le web bon nombre d'anecdotes, mais peu en français (voire pas du tout ?), et comme Boris Gourévitch est passionné par la vie des mathématiciens (serait-ce le fruit d'une frustration sous-jacente ?), il se propose de vous faire découvrir quelques-unes des histoires connues ou moins connues. Tout cela pour nous rappeler que ce sont bien des hommes eux aussi ! Décidément, Archimède se retrouve propulsé à la Une des Inclassables, hier effacé, aujourd'hui... inutile !
Décidément, Archimède se retrouve propulsé à la Une des Inclassables, hier effacé, aujourd'hui... inutile !
