Archimède, le maître de la poussée, était aussi le roi du levier, l'homme de la catapulte, et le prince la méthode d'exhaustion. Une question le concernant est cependant restée entière jusqu'à aujourd'hui: Comment a-t-il pu trouver l'encadrement suivant qui apparaît dans "De la mesure d'un cercle"?

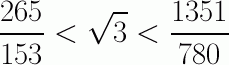
Parce que bien sûr, il n'a pas laissé le mode d'emploi et bon nombre de méthodes sont envisageables mais la candidate devrait satisfaire quelques critères de bon sens:

- La méthode utilisée ne doit faire intervenir que ce qui était connu du temps d'Archimède.

- Il doit être possible de remplacer 3 par n'importe quel autre nombre.

- Elle doit être aussi courte et élémentaire que possible.

- Elle ne doit pas impliquer d'ingéniosité  extraordinaire ni d'astuces.

Des propositions ont déjà été faites, mais aucune n'est parvenue à satisfaire tous ces critères. La méthode de Héron ne permet par exemple pas d'obtenir la valeur inférieure. Les méthodes de calcul de babyloniens n'étaient pas nécessairement connues d'Archimède. De nombreuses techniques proposées sont composites et font intervenir des méthodes différentes ou imbriquées.

Pour commencer, la méthode brute permet de parvenir au résultat. Même si elle est longue et laborieuse, cela n'implique pas qu'Archimède ne l'ait pas utilisé, mais simplement qu'elle ne vérifie pas le troisième critère. L'encadrement par deux fractions revient à minimiser la différence |m²-3n²|, et demande de dresser les listes des  m² et des 3n² jusqu'à m=1351, ce qui compte tenu de la grandeur des nombres demanderait un travail de 24 heures à raison du calcul d'un carré par minute. Il faut de plus se rappeler que la numération grecque, principalement utilisée pour les prix et les mesures, ne se prétait pas spécialement à des calculs de ce type accroissant énormément de ce fait le temps des calculs laborieux.

On peut aussi penser qu'Archimède ait résolu les équations de Pell:

Ceci au moins dans le cas particulier où n=3.

Dans ce cas, l'équation avec m=-1 ne possède pas de solution et les deux fractions satisfont :

265²-3x153²=-2 et 1351²-3x780²=1

Les babyloniens savaient résoudre ce type d'équations avec n=2 mais rien n'était dit sur la façon de la faire. Proclus écrivit qu'il en était de même pour les Pythagoriciens en utilisant un procédé algorithmique. Même si les preuves sont absentes et les écrits tardifs, rien n'empèche de le croire. Il faut cependant qu'Archimède ait été capable de généraliser le procédé avec n=3.

La méthode qui semble la plus probable car elle satisfait aux quatre critères précédents, est tout simplement une méthode d'interpolation de deux fractions qui se résume à la propriété suivante:

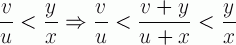
Cette propriété n'apparaît pas directement dans les Eléments mais elle peut être déduite de propositions existantes par un raisonnement géométrique sur un parallélogramme ou bien en comparant les aires de rectangles formés par les produits en croix.

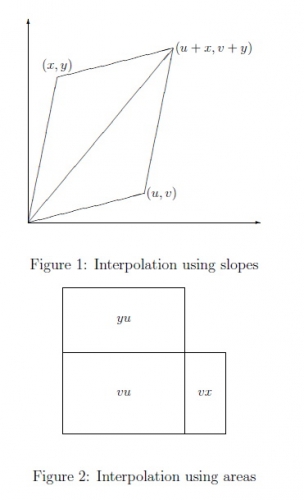
En partant d'un encadrement entre 1/1 et 2/1, 12 itérations permettent d'obtenir la valeur inférieure et avec 16, on tombe sur la valeur supérieure. De plus le calcul de la quantité m²-3n², pour chacune des fractions m/n obtenue,  permet de savoir si celle-ci est une valeur approchée par excès ou par défaut.

Il est possible que les fractions continues aient été utilisées mais rien d'une part indique que leur usage était connu en Grèce antique et de plus on retombe dans une technique identique à celle de l'interpolation.

Il semble donc que la méthode la plus probable qu'a utilisé Archimède pour réaliser cet encadrement soit la méthode d'interpolation.

Compléments : Archimedes' calculations of square roots E. B. Davies ArXiv