Représentations en mathématiques et représentations des mathématiques
L'univers des représentations m'a toujours interpellé. Les mathématiques peuvent-elles exister sans aucune représentation, sans graphique? Mon avis est que ce n'est pas possible. Quelles représentations apparaissent en mathématiques? Ou plutôt ce qui m'interesse ici serait plutôt de déterminer en quoi une représentation interpelle en mathématiques mais aussi en quoi une représentation sur les mathématiques peut aussi poser question.
Je donnerai dans ce billet un exemple de chaque.
La main de Descartes
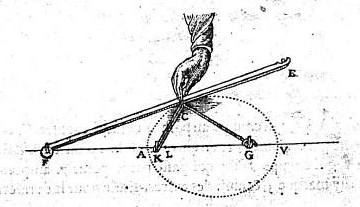
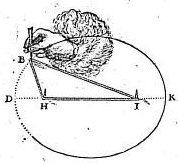
Pour ce qui est la représentation au sein de la production mathématique, on peut se poser la question de savoir pourquoi est-ce que Descartes a inclus quelques figures avec une main au milieu d'autres schémas sans aucune intervention humaine.
manière de tracer un ovale - Traité sur la géométrie - 1637
Discours de la méthode pour bien conduire sa raison et chercher la vérité dans les sciences, plus la Dioptrique, les Météores et la Géométrie qui sont des essais de cette méthode. René Descartes (1596-1650).
Les mathématiques dans la nature
Les photos de Nikki Graziano mettent en scène les mathématiques là où on ne les attend pas et suscitent l'interrogation, l'étonnement.
Représentations
J'avais, il y a quelques temps commencé de façon un peu humoristique, ce que j'avais appelé le musée du crobar. Je pense que je vais pousser un peu plus loin cette idée de l'interrogation sur la représentation et les mathématiques dans une nouvelle catégorie créée à cet effet intitulée "Représentations".