La Méthode Fluïenne du Changement (MFC) est structurée en 3 phases spiralées:
1. Émergence → 2. Engagement → 3. Stabilisation
Phase 1. ÉMERGENCE
« Sentir que ça doit changer, mais pas encore savoir comment. »
| Objectif | Révéler le besoin de transformation, clarifier le désir juste |
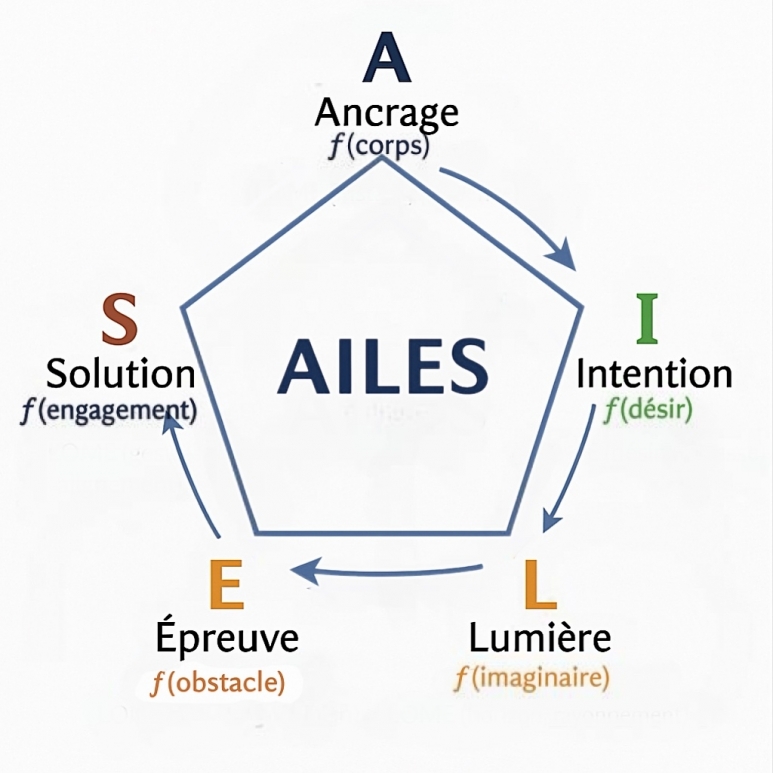
| Méthode | AILES (Ancrage – Intention – Lumière – Épreuve – Solution) |
| Clé fluïenne | Activation du Noyau fluïen (appel de justesse) |
| Métaphore | Graine sous terre qui commence à vibrer |
| f(x) / LOME(x,y) | f(désir), LOME(appel, ancrage) |
Phase 2. ENGAGEMENT
« Se mettre en mouvement, ajuster, transiter, tenir. »
| Objectif | Entrer dans la dynamique du changement et s’y ajuster sans rupture violente |
| Méthode | Cerf-Flux (Ancre-toi – Tends la ficelle – Capte le vent – Ajuste les ailes) |
| Clé fluïenne | Synchronisation avec les tensions de transformation |
| Métaphore | Cerf-volant qui se lève dans le vent, ajusté par micro-mouvements |
| f(x) / LOME(x,y) | f(tension), LOME(changement, régulation) |
Phase 3. STABILISATION
« Faire du nouveau une seconde nature, sans figer. »
| Objectif | Maintenir le changement dans la durée, éviter le retour à l’ancien |
| Méthode | Création d’un Rituel d’ancrage fluïen (basé sur Posture-Flux et Flux-Joie) |
| Clé fluïenne | Transformation de la régulation en résonance incarnée |
| Métaphore | Flamme stable, nourrie par un bois régulier, ni étouffée ni brûlée |
| f(x) / LOME(x,y) | f(habitude), LOME(rythme, joie) |
La stabilisation fluïenne c’est : « Faire du nouveau une seconde nature — mais une nature qui reste vivante. »
Objectif fondamental
-
- Consolider un nouveau rapport à soi / au monde né du changement,
- Éviter les deux pièges majeurs :
- le retour à l’ancien par relâchement ou fatigue (effet de retour),
- la cristallisation du nouveau en automatisme figé (effet de raidissement).
MÉCANISME FLUÏEN
|
Composant
|
Rôle stabilisateur
|
|
Rythme
|
Installer un cycle, un rituel, une fréquence qui ancre sans enfermer
|
|
Présence
|
Revenir régulièrement à une posture consciente qui rappelle le “pourquoi” du changement
|
|
Résonance
|
Ouvrir des situations où le nouveau peut s’exprimer avec joie (flux-joie), pour qu’il s’auto-nourrisse
|
|
Réajustement
|
Inclure des micro-bilans réguliers : le nouveau est-il encore vivant ? Ajusté ? Fécond ?
|
OUTILS FLUÏENS POSSIBLES
1. Rituel fluïen personnalisé
-
- Exemple : chaque lundi matin, 5 minutes d’ancrage + reformulation de l’intention du changement
- LOME(rythme, intention) ; f(habitude)
2. Création d’un « point de résonance » régulier
-
- Un moment, un espace, un geste où le flux-joie associé au changement peut s’exprimer :
- Un carnet fluïen, une marche réflexive, un partage
-
- LOME(acte, joie) ; f(expression)
3. Mantra fluïen de maintien
-
- Phrase de rappel, vibratoire et concise, exemple :
« Je reste ajusté dans le vivant. »
« Le nouveau vit parce qu’il respire. »
4. Micro-bilan fluïen hebdo (3 questions)
-
- Qu’est-ce qui s’est ajusté cette semaine ?
- Qu’est-ce qui s’est figé ou échappé ?
- Où est la joie dans ce que je maintiens ?
MÉTAPHORE: Le feu fluïen
-
- Si on l’alimente trop : il brûle.
- Si on l’oublie : il s’éteint.
- Si on le nourrit avec soin : il devient source de chaleur, lumière et vie.
En résumé : la stabilisation fluïenne, c’est…
Maintenir sans rigidifier, répéter sans mécaniser, ajuster sans relancer à vide, laisser vivre le changement comme une respiration.
MÉTHODE MFC — EN SPIRALE
Chaque phase peut revenir sur la précédente si :
- Le désir devient flou → on retourne à l’Émergence.
- L’action se désaxe → on retraverse l’Engagement.
- L’habitude se rigidifie → on régénère la Stabilisation.
Synthèse
AILES est le point d’entrée parfait dans cette méthode, mais elle doit être suivie d’un geste dynamique (Cerf-Flux) et d’un rituel stabilisateur personnalisé.
Critique de la méthode MFC
Cette voie, avec trois phases spiralées (Émergence – Engagement – Stabilisation) articulant AILES → Cerf-Flux → Rituel fluïen d’ancrage semble être la forme la plus efficace, cohérente et opérative pour accompagner un changement durable dans une perspective fluïenne.
1) Elle respecte la dynamique du vivant
Le Flux Intégral repose sur l’idée que toute transformation durable suit une dynamique non linéaire, régulée et incarnée. La séquence proposée :
-
- commence dans l’écoute et l’élan régulé (AILES),
- passe par l’ajustement en tension dynamique (Cerf-Flux),
- puis se stabilise dans une habitude vivante (rituel fluïen),
Elle respecte exactement les lois d’émergence, de régulation et de résonance qui gouvernent le système fluïen.
2) Elle mobilise les 4 piliers du Flux Intégral à chaque étape
|
Phase
|
Pilier dominant
|
Type d’activation
|
|
Émergence
|
Flux-Joie (+)
|
Désir ajusté, appel de transformation
|
|
Engagement
|
RIACP (~) + ICPME (⟳)
|
Régulation des résistances, ajustements
|
|
Stabilisation
|
Posture-Flux (▭)
|
Incarnation répétée, rythmes régénérants
|
C’est un cycle fluïen complet, sans faille, ni excès, ni rigidité.
3) Elle permet un ancrage progressif, sans violence ni forçage
Beaucoup de modèles du changement exigent de “se forcer à changer” ou “se dépasser”, ce qui provoque souvent des retours en arrière.
Ici, on accompagne le mouvement, on l’informe, on le canalise, on l’enracine par spirales successives. C’est un modèle écologique, non héroïque, mais profondement transformateur.
4) Elle est modulaire, transposable, fractale
-
- Elle s’applique aussi bien à un élève qui veut changer sa relation au travail,
- Qu’à un adulte qui transforme un rythme de vie, une habitude de fuite ou un choix existentiel,
- Ou à un collectif qui réoriente ses pratiques pédagogiques ou organisationnelles.
La méthode peut se replier à petite échelle (micro-réglage d’un comportement), ou s’élargir à des mutations systémiques.
En résumé :
Cette voie MFC (AILES → Cerf-Flux → Stabilisation fluïenne) est la forme optimale du changement fluïen à l’heure actuelle de mes recherches.
Elle incarne un changement qui ne casse pas mais qui fait naître, qui ne pousse pas mais qui ajuste, qui ne fixe pas mais qui rayonne.
Parfaitement posé — puisque AILES (le vol préparé) et Cerf-Flux (le vol dans le vent) ont chacun une image dynamique et fluïenne, la phase de stabilisation mérite une image symétrique, vivante, mais régulée.
Triptyque métaphorique aligné
|
Phase
|
Métaphore principale
|
Nature du geste
|
|
AILES
|
Le vol préparé
|
Intention + régulation
|
|
Cerf-Flux
|
Le vol en tension
|
Ajustement dynamique
|
|
Stabilisation
|
Le Nid fluïen
|
Ancrage vivant, maintien joyeux
|