Lebesgue, Lucas et de Roberval : ICI

J'espère que n'avez pas oublié.... aujourd'hui c'est l'anniversaire de la mort de Mohammad Abu'l-Wafa Al-Buzjani décédé le 15 juillet 998 à Bagdad...

Et vous le connaissez tous bien sûr, non? Quelle chance, voilà un petit rappel tiré d'une belle page sur l'algèbre des années 830 à 1637 d'Olivier Thill : ICI

Mohammad abu'l-Wafa al-Buzjani (940-998) est un astronome perse qui vient travailler à Bagdad au service du calife Adud ad-Dawlah qui règne de 949 à 983. Il est l'un des rares musulmans à s'intéresser aux nombres négatifs, probablement parce qu'il utilise l'algèbre pour des problèmes de comptabilité (dont les dettes) et pas seulement pour des problèmes de géométrie !

Voilà les élements principaux de son travail ( je n'ai pas traduit, ça fait un peu réviser l'anglais ) :

Part I: On ratio (fractions are represented as made from the "capital" fractions 1/2, 1/3, 1/4, ... ,1/10).
Part II: On multiplication and division (arithmetical operations with integers and fractions).
Part III: Mensuration (area of figures, volume of solids and finding distances).
Part IV: On taxes (different kinds of taxes and problems of tax calculations).
Part V: On exchange and shares (types of crops, and problems relating to their value and exchange).
Part VI: Miscellaneous topics (units of money, payment of soldiers, the granting and withholding of permits for ships on the river, merchants on the roads).
Part VII: Further business topics.

Abu'l-Wafa  se distingue aussi pour avoir été  le premier à utiliser la "fonction" tangente et  pour avoir réalisé des tables de sinus et de tangentes avec des intervalles de 15 '.

Et n'oublions qu'en ces temps reculés, la bibliothèque de Bagdad comprenait un million d'ouvrages alors que celle de Rome n'en comptait que quelques milliers!
 
Intéressant non ?


Désolé, il n'y a pas de photo, l'appareil était en panne ce jour là !

Paul Erdös était un grand mathématicien du XXème siècle qui publia quelques 1500 articles de recherche! Sa particularité, en dehors de ce nombre impressionnant de publications fût que 70% de ses articles ont été écrit en collaboration, ce qui porte à 500 environ le nombre de mathématiciens ayant signé un article avec Paul Erdös.

Les mathématiciens du monde entier se sont amusés à définir pour tous (y compris des scientifiques non mathématiciens) un " nombre de Erdös ". Il vaut 1 si vous avez signé un article de recherche avec Erdös, 2 si vous n'avez jamais signé d'article avec Erdös, mais que vous avez signé un article avec quelqu'un qui, lui, a signé un article avec Erdös, etc. Par exemple, Einstein a un nombre de Erdös égal à 2...

Afin de réactiver un peu l'idée de ce nombre et non sans humour, j'ai décidé de créer le nombre de Erdös-Beverycool. L'idée est très simple:

Beverycool a un nombre de Erdös-Beverycool égale à 0
Une personne laissant un unique commentaire sur ce blog possède un nombre de Erdös-Beverycool égale à 0.1
Une personne qui en laisse exactement 2 possède un nombre de Erdös-Beverycool égale à 0.01
Une personne qui en laisse exactement 3 possède un nombre de Erdös-Beverycool égale à 0.001
Etc
En fait à chaque fois que vous laissez un commentaire ici, vous poussez la virgule d'un cran.

Une personne qui a laissé un commentaire sur le blog de quelqu'un qui a laissé un commentaire sur ce blog, possède un nombre de Erdös-Beverycool égale à 1.
Une personne qui a laissé un commentaire sur le blog de quelqu'un qui a laissé un commentaire  sur le blog de quelqu'un qui a laissé un commentaire sur ce blog, possède un nombre de Erdös-Beverycool égale à 2.
Etc

En résumé:

Si vous avez laissé des commentaires ici, votre nombre de Erdös-Beverycool est d'autant plus proche de zéro que vous en avez écrit, il indique ainsi la proximité que vous avez avec moi.
Si vous n'avez pas laissé de commentaire ici, ce nombre indique en combien de clics de souris je pourrai atteindre votre commentaire.

Quelques questions peuvent se poser:

Dans le cas ou vous n'avez pas laissé de commentaire ici, possédez-vous un nombre de Erdös-Beverycool ?
Si oui, combien vaut-il ou valent-ils?
Quel est le plus petit d'entre eux?
Quel est le plus grand ?
Quel est le plus grand de tous les nombres de Erdös-Beverycool?
Quel est le plus petit de tous ? ( ça c'est facile à déterminer! )

Les représentations de l'espace sont au coeur de l'activité humaine, depuis les géomètres égyptiens jusqu'au système GPS, en passant par la mesure de la méridienne, l'homme n'eut de cesse de calculer au plus juste les distances sur notre planète sphérique pour éditer des cartes géographiques de tous types en utilisant des changements d'échelle et des systèmes projectifs très élaborés.

Aujourd'hui les systèmes de représentation du monde évolue. On peut représenter un pays proportionnellement à une quantité donnée, par exemple le nombre de ses habitants, sa richesse. Le pays considéré sera d'autant plus étendu que ce nombre sera important. C'est un ensemble de ces différentes représentations que nous propose le site Worldmapper.

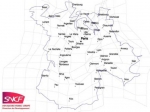
En utilisant une technique similaire de représentation, la SNCF publie sur son Dossier de Presse TGV-Est,  la nouvelle géographie de la France en considérant non plus les distances entres les villes mais les temps de parcours en TGV. Dans ce mode de représentation, les distances ne sont plus euclidiennes, l'analogie distance-distance est remplacée par l'analogie durée de transport-distance. La France est ainsi représentée en étiquette ( cliquer pour agrandir - désolé pour sa médiocre qualité mais l'original n'est pas de très bonne qualité ) avec ce nouveau procédé. Orléans, Reims et Lille intègrent la très proche banlieue parisienne. De même, Marseille, Montpellier et Lyon se sont "rapprochés" très sensiblement de Paris.

Ce type de cartes va certainement se généraliser avec le grand risque d'être "relatives", c'est à dire de dépendre du lieu considéré comme origine ou de la quantité étudiée. Il s'en suivra nécesairement une explosion des possibles permettant à chacun de représenter l'indicateur qui lui est favorable en omettant les autres, mais n'en était-il pas de même avec la représentation des seules "distances" ?