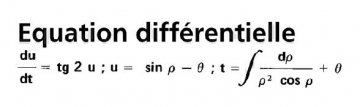Je suis d'une nature curieuse et j'ai voulu lire les articles composant le premier numéro de "Repères", le bulletin de l'IREM ( Institut de Recherche sur l'Enseignement des mMathématiques ). Ce premier numéro est paru en 1991 et je ne fut pas surpris d'y trouver un article sur la démonstration, un sur les nouveaux programmes de 6ème, un sur les géométries non euclidiennes et un sur la résolution de problèmes de second cycle, mais l'article qui attira mon attention fut le dernier de la revue. Il a été écrit pas Rudolf Bkouche qui l'intitula " Pourquoi enseigner la géométrie? ". Je ne vais pas en faire un résumé ici, mais je l'ai trouvé très intéressant. Cela me donna l'idée de faire une recherche sur Rudolf Bkouche et j'ai trouvé une page comportant de nombreux textes ICI
L'extrait suivant est tiré d'un texte de cette page " De la transposition didactique " que j'ai aussi trouvé très intéressant ( pp 22-23 ).
Premier paradoxe, la dévolution du problème.
En fait la dévolution repose sur un implicite, une forme de constructivisme qui laisse entendre que c'est à l'élève de construire son propre savoir, le rôle du professeur étant de créer la situation pour que l'élève puisse mener à bien cette construction. Déjà une première contradiction apparaît, le savoir créé par l'élève doit correspondre au savoir que l'on veut lui enseigner, il s'agit donc d'un constructivisme orienté. Il y a ici une mécompréhension de l'enseignement si l'on considère que le problème de l'enseignement est moins d'amener l'élève à construire du savoir que de lui donner les moyens d'acquérir du savoir, c'est-à-dire de faire sien un savoir qui lui est a priori extérieur; il est vrai que, posé de cette façon, l'acte d'enseignement apparaît impossible; mais cet impossible repose sur le pré-supposé constructiviste qui déclare que tout vient du sujet (mauvaise lecture de Kant pourrait-on dire) ou que le sujet et l'objet ne font qu'un (mauvaise lecture de la phénoménologie). Le constructivisme didacticien n'est alors qu'une façon de réduire le rapport au savoir à de simples jeux d'interaction, autrement dit d'éviter de le penser. Mais peut-être faut-il ici revenir sur la polémique Piaget-Chomsky qui oppose il est vrai deux dogmatismes, celui du constructivisme et celui de l'innéisme, mais le plus ouvert reste celui de Chomsky dans la mesure où il marque une confiance dans la possibilité, pour celui qui apprend, de construire à partir de l'acquis. Il y a ici deux conceptions opposées, celle du constructivisme pour qui tout savoir est construit par le sujet et celle des qualités innées (qu'il faudrait alors situer dans l'identité biologique de l'homme) qui permet à tout individu d'acquérir un savoir extérieur et de le faire sien. Le paradoxe du constructivisme est que le savoir à construire n'est pas défini par le seul individu qui apprend, il se situe dans un contexte social qui exige que celui qui apprend construise le savoir qu'on lui demande de construire; ce qui suppose le "coup de pouce" à la dévolution du problème que Brousseau présente comme un paradoxe, et il est vrai que c'en est un du point de vue constructiviste; à moins de reconnaître que la dévolution n'est autre qu'une manipulation qui doit conduire l'élève à faire ce que l'on attend qu'il fasse, la manipulation reposant sur l'illusion de l'autonomie. On comprend que dans ces conditions le professeur se sente malheureux, malheureux de ne pas laisser sa pleine liberté à l'élève dans la construction de son savoir, mais malheureux aussi lorsque, laissant toute liberté à l'élève, le contrat didactique n'est pas rempli. Dans ces conditions la didactique, poussée à ses limites, nous apprend que l'acte d'enseignement est impossible.
Deuxième paradoxe, celui des situations.
Si le savoir savant, le "vrai" savoir, est le dernier état du savoir comme on l'a vu à propos de l'étude de Marie-Jeanne Perrin sur les aires, alors tout discours qui n'est pas celui du savoir savant est un discours faux. Mais le discours du savoir savant n'est pas transparent et ne peut être compris tel quel par l'élève, il doit donc être adapté pour être compris, adaptation qui le modifie et le transforme en un savoir qui devient "non seulement approximatif, mais aussi en partie faux et inadéquat.". Le professeur doit alors choisir "entre enseigner un savoir formel et dénué de sens ou enseigner un savoir plus ou moins faux qu'il faudra rectifier." Situation paradoxale qui conduit à choisir entre le vrai et le compréhensible. Ici encore l'analyse didacticienne conduit à l'impossibilité de l'enseignement.
On pourra lire aussi " De la fin de l'enseignement " qui aborde la pédagogie du vide et le sujet des TPE.
