J'avais présenté sur ce blog le logiciel OpaleSup.
J'ai réalisé 3 cours avec:
· Le second degré
· La trigonométrie
· Les fonctions
Une lectrice du blog m'a laissé un message m'indiquant l'existence d'un autre générateur d'e-learning : Exe Learning.
J'ai utilisé ce logiciel pour produire le cours suivant:
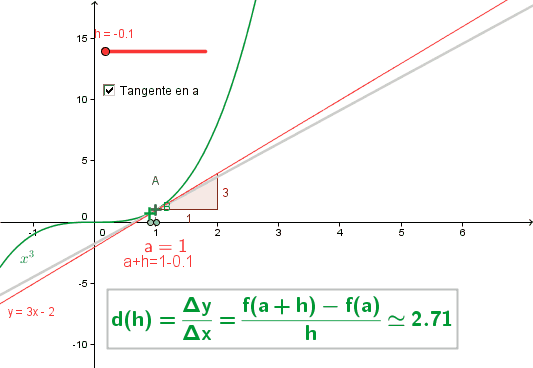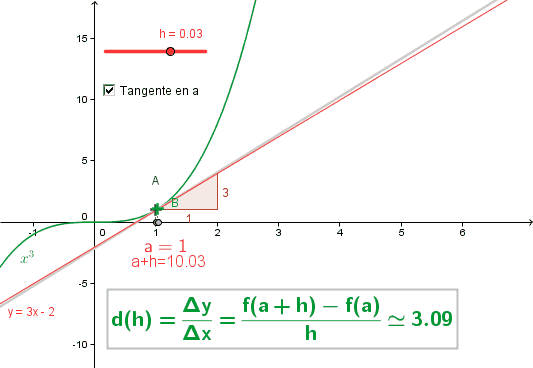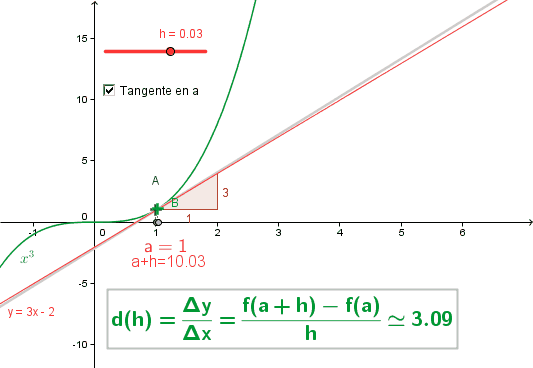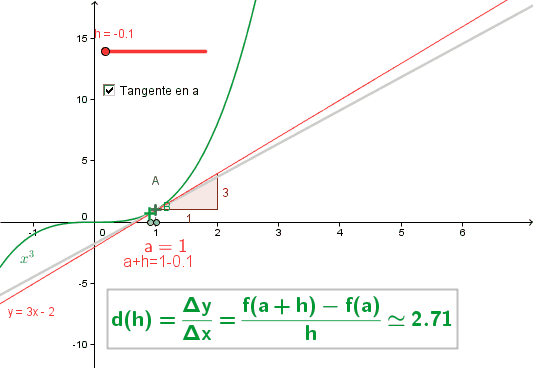
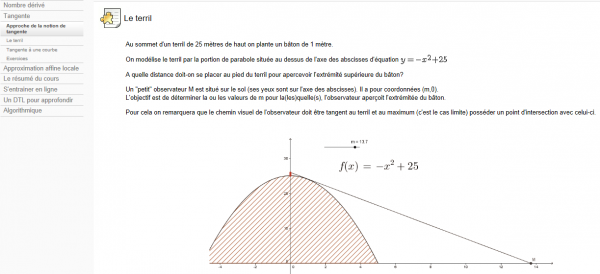
· La dérivation [I]
Exe Learning est plus souple qu'OpaleSup en ce qui concerne la présentation et la construction du cours. Il est possible de construire des modèles simples de modules. Je n'ai pas testé toutes les fonctionnalités. Le logiciel dispose des éléments principaux pour publier ses cours, écrire des mathématiques en utilisant Latex sans installation du moteur, alors qu'il le fallait pour Opale.
J'apprécie l'existence de boutons de développement pour faire apparaitre un contenu: démonstration, correction d'exercice...
J'apprécie aussi l'insertion simple de gifs animés (réalisés avec GeoGebra 4). Par contre l'insertion d'applets GeoGebra renvoie des messages d'erreurs intempestifs qui parviennent parfois à planter le logiciel. J'ai donc préféré le gif animé et lorsque la manipulation du fichier GeoGebra est intéressante, le couplage Gif animé+fichier sur GeoGebraTube.
Il existe la possibilité d'éditer des flux RSS mes ceux-ci ne semblent pas s'actualiser. C'est surprenant.
L'icône de bureau est particulèrement laide... on dirait une sorte de mouche grise avec deux gros yeux.
Même si l'édition papier d'Opale n'est pas parfaite, celle-ci est d'une qualité sans commune mesure avec le fichier texte d'exe learning. Inutile donc de songer à réaliser une version papier des cous réalisés avec Exe Learning.
Malgré ces quelques inconvénients, je pense que je vais préférer Exe lLarning pour poursuivre la publication de mes cours, simplement parce que la présentation finale me parait plus sympa et la construction des modules est beaucoup plus naturelle...
Affaire à suivre pour vous, lecteurs de ce blog, qui me suivez depuis longtemps et savez certainement que je suis particulièrement interessé par la publication de mathématiques en ligne...