Le débat scientifique en classe.

La parole à .... Liouba Leroux et Thomas Lecorre ( PDF ) : ICI

C'est une conférence donnée à l'IAP le 4 septembre 2007 par par Hervé Le Treut, directeur du laboratoire de météorologie dynamique du CNRS qui effectue une mise en relief des variations climatiques suivant les différentes échelles de temps et d'espace et explique ce phénomène complexe de  façon extrêmement claire.

La conférence est téléchargeable et diffusée sur le site du CERIMES : ICI

Une synthèse de la première heure

L'augmentation de carbone et des gaz à effet de serre est un phénomène récent et d'une grande ampleur dont les effets sur le climat sont différés. C'est vers les années 1970 que le taux de carbone dans l'atmosphère à passé le seuil critique de "non traitement" par la planète. Il correspond en fait au taux actuel produit par un chinois de 0.5 tonne par an et par habitant, un européen en produit 3 et un américain 6. Cette augmentation brutale du niveau de carbone est un phénomène inédit de l'histoire climatique sur le dernier million d'années. Le système est en fait très équilibré dans la régulation du cycle du carbone et brasse environ 150 milliards de tonnes. La production actuelle humaine, qui est de l'ordre de 7 milliards de tonnes, peut sembler faible mais "permet" à ce système équilibré de se déséquilibrer. L'effet de serre est dû à moins de 1% de la masse totale de l'athmosphère et pour se donner une image, il est impossible de faire avancer un camion avec le pied sauf si le pied est placé au bon endroit, c'est à dire sur l'accélérateur.

Historiquement les modèles ne s'ont pas été conçus pour étudier le réchauffement climatique mais pour modéliser le climat avec les équations de mécanique des fluides et permettre de "construire" un objet informatique qui soit le plus près possible de la planète réelle. Le temps de calcul pendant ces mêmes années a fortement diminué, lorsqu'un calcul nécessitait un week-end aux début de l'ère informatique, il ne nécessite plus aujourd'hui que quelques dizaines de secondes.

Ce que nous donne un modèle c'est l'état de l'atmosphère environ toutes les 10 minutes, en faisant la "moyenne" de ces modèles on regarde si le résultat obtenu sur la planète " modèle" et le même que sur la planète réelle. On a construit ue planète qui est de plus en plus ressemblante à la planète réelle dans les dernières décennies. 80% du travail fait autour des modèles climatiques est occupé pour leur validation avec les observations effectuées. Un modèle est le fruit du travail d'une équipe de 50 à 100 personnes depuis plus d'une dizaine d'années. Il existe sur la planète une quinzaine de modèles différents correspondant au "tour de main de l'artisan" qui en est à l'origine. Pour faire des prévisions, ces modèles doivent prendre en compte l'activité humaine. Différents scénarios de référence ont été établis par le GIEC pour effectuer ces prévisions.

Les ordres de grandeur sont très importants, même s'il s'agit de 2 degrés. Ce que l'on voit là n'est que le début d'une série de phénomènes beaucoup plus violents.

Les prévisions faites dans les années 90 avec des modèles plus simples donnent des résultats de même nature qu'avec les modèles actuels plus précis.

Je vous laisse découvrir les 40 dernières minutes de la conférence par vous-même.


La sensibilité des modèles, un article du Monde: ICI

Quel sera le climat de la Terre lorsque la concentration atmosphérique en CO2 aura été multipliée par deux par rapport à l’époque préindustrielle? Cette question est un Graal pour les climatologues et leur réponse est très attendue par les décideurs politiques. Pourtant, si l’on en croit deux chercheurs qui publient une analyse aujourd’hui dans la revue Science, il vaudrait mieux laisser tomber cette quête et s’habituer à vivre dans l’incertitude. Gerard Roe et Marcia Baker, de l’université de Washington (Seattle, USA), estiment en effet que les incertitudes sur la réponse du climat aux changements atmosphériques sont trop grandes pour que les scientifiques puissent fournir des prédictions plus précises que les fourchettes actuelles.

Selon les données retenues par le Groupement intergouvernemental d’étude sur le climat (Giec/Ipcc), les températures augmenteront de 2°C à 4,5°C en cas de doublement de la concentration atmosphérique de dioxyde de carbone. Si la fourchette basse encadrant cette sensibilité du climat a été affinée en 30 ans, la précision de la fourchette haute n’a pas beaucoup bougé, malgré des années de recherches et de modélisations sophistiquées, relèvent Roe et Baker. Se livrant à un complexe exercice mathématique, ces deux chercheurs tentent de modéliser l’incertitude inhérente à la sensibilité climatique afin de faciliter la tâche de leurs collègues climatologues.

Le problème vient des réactions climatiques liées au changement –ce qu’ils appellent le feedback. Que se passera-t-il lorsque la température aura augmenté de 4°C? De nombreux mécanismes seront modifiés : certains accélèreront le réchauffement, d’autres le freineront. Dans ce domaine, les petites incertitudes des processus physiques sont très largement amplifiées par les mécanismes climatiques, expliquent Roe et Baker.

Tout en espérant que leur équation facilite la recherche, les deux auteurs concluent que plus le réchauffement sera important, plus le feedback sera amplifié et plus le degré d’incertitude sera grand.

Pour compléter le tag " modélisation des évènements terrestres" de ce blog ( contient cette note ! ) ICI

Le Café Pédagogique cite deux blogs de profs de maths, celui de Guy Marion et le mien. Mille Mercis et c'est ICI

Un nouveau modèle de marée, régional et haute résolution, a été développé pour la région australe de l'océan Indien. Il a permis d'améliorer nettement la simulation des marées dans les zones côtières, ainsi que sous la plate-forme de glace d'Amery en Antarctique. Ce modèle permettra à l'avenir de mieux corriger les données satellitaires des effets de la marée dans cette région. 

La comparaison des composantes de marée (amplitudes et phases) observées, issues de données GPS et de marégraphes, et modélisées met en évidence que ce nouveau modèle donne des résultats plus proches de la réalité que les modèles précédents et permet donc d'améliorer la connaissance de la marée dans cette région et de ses effets sur les plates-formes de glace.

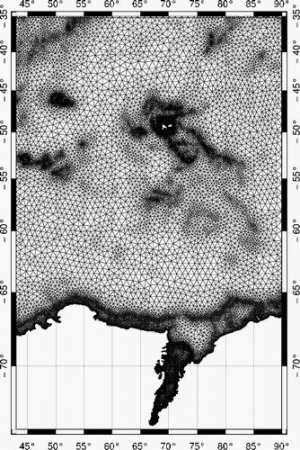
 Maillage utilisé pour la simulation de la marée.

L'article de Techno-sciences : ICI

Il est assez rare sur ce blog que je parle de moi mais ma journée d'aujourd'hui concerne les maths alors je vais en toucher quelques mots ici. Il y a bien longtemps que je n'étais pas allé à Paris et c'est ce que j'ai fait aujourd'hui. Dans le train, je m'assois au centre du wagon, là où il y a une zone de quatre sièges se faisant face deux à deux. Après avoir parcouru quelques kilomètres le train s'arrête et s'assoient à coté de moi trois personnes. Le hasard fait que c'étaient des mathématiciens qui je l'avoue parlaient presque une langue étrangère et si je dis cela ce n'est pas parce qu'ils échangeaient leurs idées en anglais...  Ils revenaient en fait d'un colloque et après qu'ils aient constaté la difficulté de leur sujet d'étude, je leur adressais la parole et nous passâmes le reste du trajet à nous amuser car, dans le groupe, l'anglais était un joyeux luron. Arrivé à Paris, j'ai réemprunté les chemins que je fréquentais lorsque j'étais étudiant pour me diriger vers le panthéon où se tenait la manifestation ( qui n'est pas terminée ) organisée par le magasine Tangente. J'ai fait de belles photos du polyèdre géant qui se trouvait devant le Panthéon et la Sorbonne mais je ne pourrai malheureusement pas vous les montrer car celles-ci sont définitivement perdues suite à un problème technique inexplicable ayant touché ma caméra. Je me suis approché du hall de la mairie du Vème où je suis entré pour la première fois aujourd'hui, après être passé un nombre incalculable de fois devant. Au deuxième étage , j'ai rencontré Gille Cohen, Directeur du magazine  et me suis fait dédicacé le livre " Les contre-exemples en mathématiques " par son auteur Bertrand Hauchecorne.

Pour conclure, je ne peux vous engager qu'à imaginer un polyèdre géant dont les arêtes sont des baguettes de bois au travers duquel j'ai photographié dans la direction du jardin du Luxembourg et de la rue Soufflot, la tour Eiffel. Je me suis ensuite tourné vers la faculté de Droit dont le sigle apparaissait entre les arêtes, puis en contre-plongée j'avais immortalisé avec le polyèdre, le fronton du Panthéon sur lequel est inscrit en lettres d'or, comme chacun le sait....

 Aux grands hommes la patrie reconnaissante 

Alors j'ai pallié le manque par cette reconstitution approximative!