La cycloïde, la chaînette et le cercle font leur film (de savon)
Il est assez de rare de trouver un traitement très "pédagogique" d'un sujet au sens noble du terme, c'est à dire permettant de l'éclairer sous des angles très différents, dont un très original et concret, tout en construisant son unité profonde.
Prenons ensemble l'optique, la dynamique, la statique, la géométrie, l'élasticité, le calcul différentiel et l'histoire des mathématiques. Prenons aussi trois courbes très connues, la cycloïde, la chaînette et le cercle. Il semble difficile de relier le tout en un ensemble cohérent et pourtant il suffit d'un peu de savon pour les regrouper!
Je vais tenter d'expliquer. En cas de dérapage et pour plus de détails, l'article original est ICI et il suffit de s'y référer.
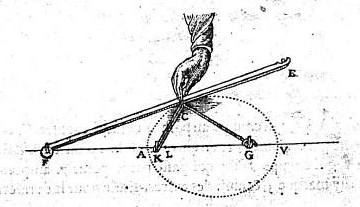
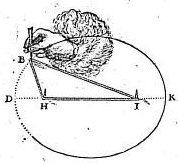
L'histoire commence par la recherche de la brachistochrone, c'est à dire de la courbe de descente la plus rapide pour un point pesant. En 1697, Jacques Bernouilli pose ce problème. Newton, Leibniz, Jacques et son frère Jean Bernouilli s'y collèrent et proposèrent leur solution. Les deux frères (qui se haïssaient) y parvinrent et découvrirent que le profil cherché était une portion de cycloïde.
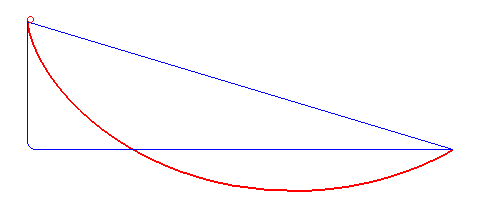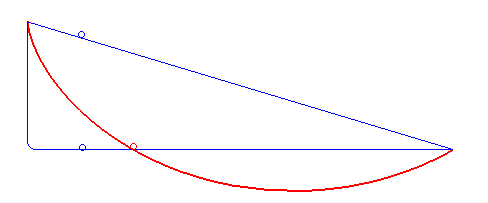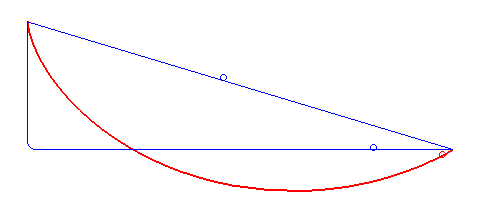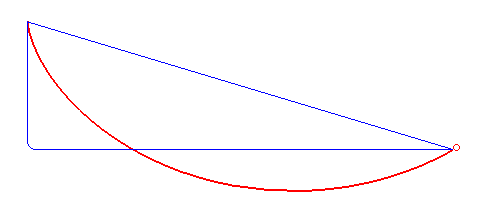
Un peu plus tard, ce problème peut être résolu grâce au calcul différentiel en recherchant le minimum d'une expression du type fonctionnelle qui a été étudiée par Euler et Lagrange.
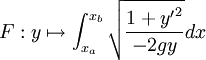
Prenons un peu de recul:
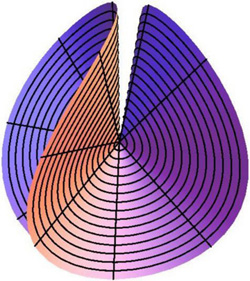
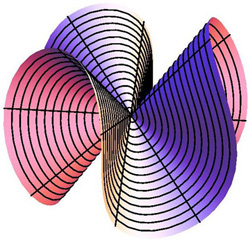
En fait l'idée c'est de penser à une bulle de savon. Il faut aussi avoir l'idée de planter deux piquets verticaux entre deux profils: l'un horizontal z=0 et l'autre z=1/√y. En plaçant un film de savon entre les piquets et les deux surfaces on devrait voir cela:

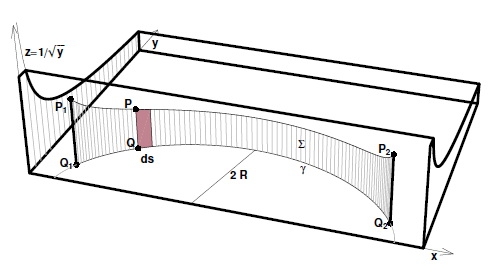
La trace laissée sur la surface horizontale est une cycloïde. Pour faire un peu plus scientifique on peut dire que la courbe qui minimise la surface de la bulle de savon ( oui la bulle de savon est fainéante, elle suivra toujours ce que l'on appelle une surface minimale) est la même que celle celle qui minimise le temps de parcours d'un point pesant.
Pourquoi me direz-vous? Tout simplement parce que le problème mathématique associé aux deux problèmes est similaire et donc la solution est de même nature.
Et pourquoi le problème mathématique est de même nature? Tout simplement parce que le profil z=1/√y a été bien choisi.
L'élasticité, est maintenant mariée à l'histoire des maths, au calcul des variations et à la dynamique.
On pourrait aussi s'imaginer qu'un rayon lumineux circule du point P1 au point P2 dans un milieu dont l'indice de réfraction serait proportionnel à 1/√y. La courbe suivie par le rayon lumineux serait identique à la courbe précédente: une cycloïde. Et voilà donc l'optique qui se mèle à la partie.
Supposons maintenant qu'une chaine soit tendue entre deux points dans un lieu où le potentiel de gravitation (très particulier, certes) serait proportionel à 1/√y . La courbe formée par le fil serait une cycloïde. La statique s'invite.
L'intérêt de ce dernier point est de retrouver le profil de la chaînette avec un film de savon en choisissant un profil de type z=ky. C'est la courbe qui minimise son énergie lorsqu'elle est soumise à la pesanteur.

Pour trouver le cercle, il suffit de changer le profil supérieur et le choisir tel que z=1/y. En reprenant les analogies précédentes, les trois courbes: la cycloïde, la chainette et le cercle se retrouvent ensemble dans le même "bain" (à bulles).
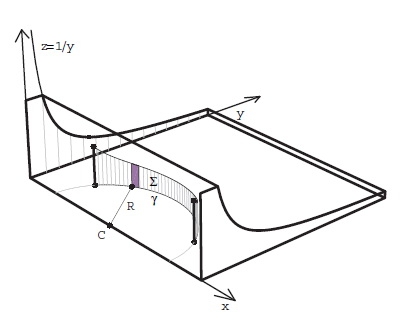
Voilà, c'est terminé et pour compléter quelques adresses suivent:
Autour de la cycloïde "Maths en Jean"
Complètement cycloïdique "Blog Sciences"
Courbe brachistochrone "Mathcurve"
Brachistochron Problem "Wolfram"
Courbe Brachistochrone "Wikipédia"
Solving the brachistochron and other variational problems with soap films "ArXiv"
Soap films help to solve mathematical problems