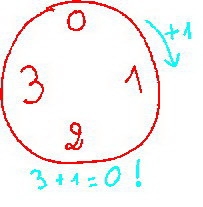Vérité , axiome, postulat et René s'invite à la maison.
Leibniz disait " Qu'un et un font deux, ce n'est pas une vérité mais la définition de deux". Alors qu'est ce la Vérité si 1+1=2 passe au rang de définition et perd son statut de vérité ? La question mérite d'être posée mais j'ai bien peur de rendre encore plus dense le problème initial.
D'une façon plus générale, ajouter un à un nombre donné serait donc un axiome avant d'être une vérité. Nous pouvons donc nous demander à juste titre ce qu'est un axiome. Alors là je suis un peu allé voir ce que disait le dictionnaire. J'en ai pris un au hasard, en fait pas tout à fait, c'est le seul dont je dispose: le Maxidico, mais si, rappelez vous, c'était le dico à 99 Frs de MaxiLivre, il avait été interdit.... Enfin bref, nous avons le choix entre : "Proposition reçue pour vraie sans le recours d'une démonstration du fait de sa primauté psychologique oude sa primauté logique" ou " Dans un système hypothético-déductif, toute proposition qui ne se déduit pas d'une autre et qui est posée par hypothèse, en vue d'une démonstration".
Sommes-nous plus avancé ? J'ai la conviction que non car la première définition nous ramène à la Vérité déclarée comme évidence et la deuxième définition nous invite à penser que 1+1=2 est une proposition. C'est pourtant sur cette deuxième assertion que nous allons nous appuyer pour poursuivre. En effet, il n'y est aucunement mention d'une vérité quelconque mais d'un point de départ sur lequel repose le raisonnement hypothético-déductif. L'axiome serait donc d'une part initial et d'autre part universel ce qui ferait sa différence avec le postulat qui aurait un caractère plus local, plus temporel, même si ce n'est pas aussi net dans le dictionnaire. Le postulat serait à l'axiome ce que la vérité ou la véracité serait à la Vérité, si j'ai bien compris.
En fait, chez les mathématiciens-philosophes grecs, un postulat est un principe d'un système déductif qui ne peut-être utilisé sans l'accord de l'interlocuteur. Si ce dernier accepte le postulat, il doit en accepter toutes les conséquences, et les résultats qui en découlent. Et à l'inverse, si on le refuse, il faut abandonner toutes les conclusions qui en découleraient. En résumé, si vous invitez votre copain René chez vous, vous devez en accepter toutes les conséquences y compris les plus lourdes ( entre autres qu'il s'invite tout seul ! ) et si vous le laissez à la porte , ne venez pas pleurnicher qu'il ne vous aidera pas en cas de difficultés.
Revenons à notre problème initial concernant la confusion entre vérité, axiome et postulat. Je dirais que chez les grecs 1+1=2 était une vérité, chez les algébristes, il devenait axiome et à l'ère de l'informatique il se réduit à un postulat, localement vrai mais certainement beaucoup moins général que la célèbre table de Vérité de l'addition binaire que je rappelle : 0+0=0 ; 1+0=0+1=1 et le fameux : 1+1=0 sans lequel nos ordinateurs auraient bien du mal à fonctionner !!!!
Et si l'on vous prend pour le roi ( ou la reine) des imbéciles d'énoncer que 1+2 = 5, n'oubliez pas que la personne qui prendra son téléphone portable ou son ordinateur pour communiquer votre folie à son proche entourage, aura accepté, mais elle sans le savoir, que 1+1=0 et comme un homme averti en vaut 2 vous voilà bien paré pour lui démontrer ce que vous voulez!
La difficulté n'est donc pas tant d'accepter une "Vérité" ou une "Non-Vérité" mais bien d'accepter toutes les conséquences qui en découlent.
Accepter que 1+1=2 est plus naturel que d'accepter que 1+1=0 mais la deuxième proposition n'en reste pas moins valide. Veillons donc à ne pas confondre Vérité et acceptation implicite de conséquences visibles.
Merci Leibnitz.
Le postulat - la méthode d'exhaustion PDF d'André Ross : ICI
Les axiomes en mathématique selon Blanché : ICI
Citations de Blanché : ICI
La méthode axiomatique et la philosophie : ICI
Citations logique et mathématiques : ICI