En décembre 2010, je publiais sur le Wiki que j'avais initialement destiné à des cours de mathématiques interactifs, un article intitulé "l'apprentissage fractal".
L'idée était alors, que les besoins d'apprentissage de l'apprenant (par nature non identifiés précisément puisque leur regroupement est souvent hétérogène), ne coïncidaient que très rarement sur le long terme avec les séquences d'enseignement. L'optimisation me semblait donc possible en "fractalisant" les séquences d'enseignement. Pour cela il suffisait de respecter temporellement les trois principales phases de l'apprentissage (découverte et automatisation, fonctionnement et méthodes, synthèse et liens) en leur ajoutant une dimension fractale, c'est à dire en redécoupant chacune de ces trois phases par les trois autres. Une méthode d'enseignement fractale voit ainsi le jour faisant intervenir sciemment une certaine verticalité locale et globale des contenus ainsi qu'une diversification des approches. J'avais créé une petite animation en considérant un enseignant décrivant successivement ces trois phases au contact d'un étudiant aux besoins d'apprentissage non définis.
L'apprenant et ses besoins d'apprentissage est au milieu, le professeur "non fractalisé" en haut, et le professeur "fractalisé" en bas:
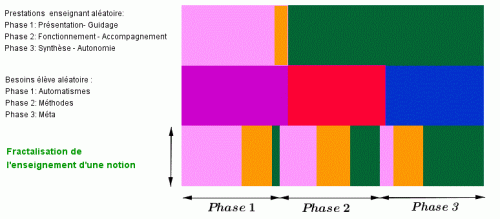
L'apprenant possède ici des besoins équilibrés, le professeur du haut est plutôt "binaire" (présentation des notions - concepts évolués), ne laissant que peu de place à un enseignement intermédiaire. La "fractalisation" (en bas) de l'enseignement optimise en moyenne les contacts d'apprentissage.
Il est sans doute possible d'aller un peu plus loin dans ce modèle, en faisant intervenir la nature fractale des besoins d'apprentissage et en ne considérant plus seulement qu'ils se délimitent à trois phases temporelles clairement identifiées.
Cette rugosité fractale entre d'ailleurs dans le langage courant en disant par exemple que les savoirs glissent, que l'enseignant n'a pas de prise, ou qu'au contraire l'élève capte intégralement le discours du professeur, accrochant ainsi tout ce qu'il trouve sur son chemin. D'une surface modélisée comme lisse à une surface accrochant jusqu'aux concepts les plus abstraits ou complexes, le paysage fractal de l'apprentissage peut trouver sa représentation aussi bien dans un lisse bourgeonnement que dans un système montagneux qui retient tout au passage. Le bourgeonnement peut s'avérer lent ou rapide, et la montagne friable ou granitique.
Dans tous les cas l'image d'un frottement entre l'apprenant et l'enseignant, apparaît. Toutes les rugosités d'enseignement ne peuvent fonctionner sur celles de tous les apprentissages. La diversité semble donc bien être la base de l'optimum recherchée. Cette diversification se fait, non pas sur les contenus (progression spiralée par exemple, dilution), mais sur les approches!

Cette notion de rugosité d'apprentissage et de glissement est à définir. On pourrait peut-être s'imaginer une diminution de cette rugosité au fur et à mesure que l'on itère la construction fractale. En effet, les concepts abstraits peuvent être considérés comme très saillants, alors que l'approche concrète serait plus douce et donc de grain plus fin. L'analogie mécanique s'arrête donc là et celle du langage courant aussi (personnage grossier par exemple). Les surfaces d'apprentissage et d'enseignement sont d'autant plus adhérentes l'une à l'autre qu'elles sont au même degré de "fractalité", au même nombre d'itérations. Nous voyons ici que l'objectif d'apprentissage optimal serait celui associé à la première itération, ou même à son absence. L'objectif recherché par tout pédagogue, serait que chaque élève accède à la "simplicité" d'apprentissage du premier flocon, symétrique et triangulaire, comme une dent acérée dévorant toute difficulté conceptuelle. Le flocon neigeux fortement itéré, serait quant à lui synonyme d'éloignement, de "trop plein de", d'affectif, d'immédiateté, etc...
L'analogie précédente possède l'avantage de sortir les difficultés d'apprentissage de l'ornière de la notion de manque et d'insuffisance, et de les ramener vers une "géométrie" de la surface, pour laquelle l'enseignant pourrait construire un outil, une sorte de râpe dynamique dont il ferait varier le grain, la vitesse de passage et la force d'appui.
Les stratégies de remédiation, de soutien offertes par le système se trouvent de facto remplacées par des stratégies d'adaptation à la surface, de modification du terrain, et de quantification fractale. C'est sans doute ce qui est fait aujourd'hui pendant ces heures dites "différenciées", "individualisées", "personnalisées", mais la notion de manque à combler a disparu ici, pour laisser place à celle de matière à "travailler" en remplaçant une granulosité fine par une autre qui le serait moins, au moins localement.
Les difficultés d'apprentissage (fractalité fine et peu profonde, aspect globalement poli et localement rugueux) ne devront se trouver en contact qu'avec une forme d'enseignement similaire, au moins jusqu'au déclenchement de la modification durable de la géométrie. Un angle trop saillant... et c'est l'accroc!
Un profil qui conceptualise et abstrait très rapidement pourra se trouver en contact avec un profil d'enseignement plus "abrupt". Il reste impératif de ne pas confondre, compréhension et restitution. Combien d'élèves possèdent un profil d'apprentissage donné mais avec une restitution ou une compréhension profonde plus difficiles. La géométrie de la surface d'apprentissage, doit aussi tenir compte de l'impératif de restitution sous une forme imposée (langage, écrit, processus, graphique, analogie....).
Ce qui me parait intéressant dans cette histoire, c'est la généralité de cette approche à tous les profils. J'ai aussi trouvé une modélisation fractale (au niveau des besoins d'apprentissage), dans la littérature : "Identifier des besoins d'apprentissage" par Valérie Barry, qui enseigne dans les formations pour l'adaptation scolaire et la scolarisation des élèves handicapés. Je n'avais pas lu le livre lorsque j'ai construit les premières marches de mon idée d'apprentissage fractal (le livre est sorti en 2011 !). Ceci me laisse à penser que la piste "fractale" a le mérite d'être explorée. J'ai pour ma part en face de moi, un public relativement favorisé, socialement comme scolairement, ce qui ne m'empêche pas de voir des élèves en difficultés dans leur parcours et dans leurs apprentissages. J'ai développé de mon coté cette approche auprès d'élèves qui feront tous, pour la plupart, des études supérieures longues. Elle semble aussi pouvoir être pertinente pour aborder les difficultés d'apprentissage.
Je vais donc tenter d'affiner mes réflexions et de faire varier la rugosité de ma râpe pédagogique à l'avenir, afin de trouver encore quelques leviers intéressants.
C'est en écoutant une conférence de Serge Boimare que m'est venue cette image de la râpe fractale, que l'on pourrait qualifier d'outil-problème plus que d'outil-solution pour reprendre une expression du livre de V. Barry.
J'écoutais Serge raconter comment il attaque méthodiquement, avec une voix douce et des contes, l’extrême dureté de l'intellect des enfants qu'il a devant lui, et qui ne lui offrent que très peu de prise, même pas de rester dans la classe. Alors tous les jours, inlassablement sans doute, faut-il effectuer la même démarche avec des outils de fine rugosité, sans lasser, sans trop appuyer afin de faire naître quelques aspérités plus marquées à la surface de ces apprenants difficiles, ou faire apparaître une surface dépolie, sur lesquelles on peut commencer à construire, à abstraire, à modéliser, à anticiper. Dès ses premiers mots les difficultés d'apprentissage ne sont plus vues comme un manque, mais comme un empêchement de penser, et je rajoute comme si il y avait une gangue à élimer avant de trouver un terrain plus tendre. L'outil s'adapte au fil des jours, synchronisé sur l'état des apprenants. Alors à petit pas certainement, l'apprentissage dessine quelques formes plus vastes, vite recouvertes par les premières feuilles qui tombent mais laissant, au hasard des jours, une base sur laquelle il est sans doute possible de s'appuyer un peu pour poursuivre le travail.
Afin de ne pas commettre de contresens sur la rugosité d'apprentissage et d'enseignement, je tiens à préciser que, pour moi, cette rugosité est d'autant plus marquée que l'itération du processus fractal est faible. Ainsi, le premier triangle du flocon de Von Koch, constituerait pour moi un profil très grossier et donc très accrocheur, alors que les itérations successives montrent un adoucissement de la "saillance". Dans le schéma suivant, le profil d'apprentissage le plus difficile est celui qui est en haut. Il correspond à une rugosité fine et à un nombre d'itérations important. Celui du bas est au contraire très "coupant", et peut être mis au contact d'une forte conceptualisation. L'apprentissage est ici vu comme un acte d'épure avant d'être considéré comme celui d'un remplissage, qui s'avère être secondaire, et non entravé dès que le profil requis est atteint.

Cette modélisation a le mérite d'introduire une image plus réelle de la réalité de l'apprentissage qui voit les freins comme un recouvrement, un rapprochement du concret et de l'affectif. En ce sens le "bon apprenant" est déjà celui qui a su faire un chemin inverse de dé-itération et non pas de remplissage, comme on l'imagine usuellement. La symbolique de l'apprentissage est donc renversée puisqu'il est plus question ici d'épure et de vide, que de remplissage, ce dernier ne survenant que lorsque la géométrie de surface de l'apprenant coïncide avec celle de l'enseignant.
En écrivant ces lignes, je m'aperçois aussi que cette modélisation "colle" avec mon expérience, celle de constater la présence d'un brouillard affectif pouvant avoir raison de tout apprentissage, et aussi de la nécessité du travail sur cette porte d'entrée pour tout apprenant en difficulté et ceux en bas âge. C'est aussi sans doute pourquoi, l'anxiété d'apprentissage prend souvent la forme de la mise à nu, de l'invasion intérieure, de la perte de défense chez les plus fragiles.
Ainsi donc à tous les stades de l'apprentissage et quelque soit le profil de l'apprenant, la modélisation fractale semble ouvrir un champ symbolique et conceptuel dont il serait dommage de se priver. Reste sans doute quelques recherches à faire, à quantifier et sans doute un vocabulaire à affiner...


