Origami
-
-
Du papier et des maths
Quelques symétries et autres fractales, une magnifique galerie flikr des maîtres de l'origami à visiter ICI
C'est un modèle de Jun Maekawa qui est d'ailleurs l'auteur d'un théorème qui porte son nom :
If one looks inside a flat origami without unfolding it, one sees a zigzagged profile, determined by an alternation of "mountain-creases" and "valley-creases." The numbers of mountains and valleys always differ by 2.
-
Des fêtes de fin d'année studieuses ( ou presque )
Quelques idées pour petits et grands...
Réaliser et colorier ses mandalas
Plus de 5000 idées d'activités et bricolage sur tête à modeler
Illusions d'optique ( liste de sites )
Et tous les jeux sélectionnés PAR DEUX EXCELLENTS blogs de Maths du Web : Blog à maths, et Le Coyote
Il y a certainement des centaines d'autres idées en rapport plus ou moins étroit avec les mathématiques, utilisez ce moteur de recherche dédié aux mathématiques, il vous permettra de mieux cibler vos recherches. -
Origamis et mathématiques
 La complexité mathématique de cet art japonais ancestral est de savoir si étant donné le tracé de plis sur une feuille de papier, celle-ci se pliera effectivement avec des formes planes localement, sans l'apparition d'autre pli. C'est ce qu'indique Ian Stewart pour introduire la naissance d'une nouvelle forme d'Origamis d'origine mathématique , "le Pinecone ".
La complexité mathématique de cet art japonais ancestral est de savoir si étant donné le tracé de plis sur une feuille de papier, celle-ci se pliera effectivement avec des formes planes localement, sans l'apparition d'autre pli. C'est ce qu'indique Ian Stewart pour introduire la naissance d'une nouvelle forme d'Origamis d'origine mathématique , "le Pinecone ".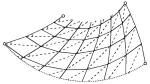
Dans le diagamme précédent, les lignes continues doivent être interprétées comme des arêtes et les pointillés comme des creux ( ou vallées).
C'est presque la même structure ( mais pas la même) que l'on retrouve fréquemment en phyllotaxie.
L'intégralité de l'article sur la page "Math in the media" de l'American Mathematical Society : ICI
-
Origamic Architecture

Le site de Origamic Architecture : ICI
