Origamis et mathématiques
 La complexité mathématique de cet art japonais ancestral est de savoir si étant donné le tracé de plis sur une feuille de papier, celle-ci se pliera effectivement avec des formes planes localement, sans l'apparition d'autre pli. C'est ce qu'indique Ian Stewart pour introduire la naissance d'une nouvelle forme d'Origamis d'origine mathématique , "le Pinecone ".
La complexité mathématique de cet art japonais ancestral est de savoir si étant donné le tracé de plis sur une feuille de papier, celle-ci se pliera effectivement avec des formes planes localement, sans l'apparition d'autre pli. C'est ce qu'indique Ian Stewart pour introduire la naissance d'une nouvelle forme d'Origamis d'origine mathématique , "le Pinecone ".
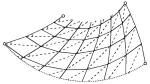
Dans le diagamme précédent, les lignes continues doivent être interprétées comme des arêtes et les pointillés comme des creux ( ou vallées).
C'est presque la même structure ( mais pas la même) que l'on retrouve fréquemment en phyllotaxie.

L'intégralité de l'article sur la page "Math in the media" de l'American Mathematical Society : ICI